网友您好, 请在下方输入框内输入要搜索的题目:
设随机变量X~B(1,0.8)(二项分布),则X的分布函数为___________.
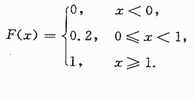
设随机变量X服从标准正态分布,则其密度函数φ0(x)=
答案:因为是标准正态分布,分布函数关于y轴对称,Ф(0)刚好是y轴左半部分面积.因为总面积为1(总概率为1),面积的一半,即Ф(0)=0.5.
则数学期望E(X)等于( )。



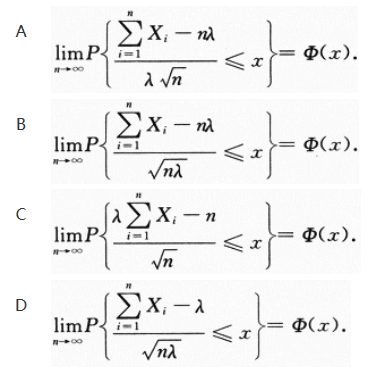
选择性必修第三册 随机变量及其分布基础回归扎实练一、选择题1.(2021全国高二课时练习)设随机变量的正态分布密度函数为,则参数,的值分别是()A,B,C,D,2.已知,则等于( )ABCD3.有一批种子的发芽率为0.9,出芽后的幼苗成活率为0.8,在这批种子中,随机抽取一粒,则这粒种子能成长为幼苗的概率是()A0.72B0.8C D0.94.若在一次测量中出现正误差和负误差的概率都是,则在5次测量中恰好出现2次正误差的概率是()A. B. C. D.5. 袋中装有大小相同的5个球,分别标有1,2,3,4,5五个号码,现在在有放回的条件下依次取出两个球,设两个球的号码之和为随机变量,则所有可能取值的个数是()A25B10C15D96.一袋中装有10个球,其中3个黑球、7个白球,从中先后随意各取一球(不放回),则第二次取到的是黑球的概率为()ABCD7.若随机变量的分布列如下表所示,则的值为()1230.2A0.1B0.2C0.3D0.428.(2022全国模拟预测)同时抛掷两枚质地均匀的硬币一次,若两枚硬币都正面向上,就说这次试验成功,则3次试验中至少有2次成功的概率是()ABCD二、填空题9.若,则_10.设随机变量X的分布列,则常数a的值为_;_11.(2022吉林东北师大附中高二期末)某n重伯努利试验中,事件A发生的概率为p,事件A发生的次数记为X,则_12.某人外出出差,委托邻居给家里植物浇一次水,设不浇水,植物枯萎的概率为0.8,浇水,植物枯萎的概率为0.15邻居记得浇水的概率为0.9则该人回来植物没有枯萎的概率为_三、解答题13.已知一个不透明的口袋中有4个白球和8个红球,球除颜色外完全相同.(1)若一个人从口袋中随机抽取一个球,求其抽取到白球的概率;(2)若一个人从口袋中随机不放回连续抽取球两次,每次抽取一个球,求在第一次抽取出白球的条件下第二次抽取出的也是白球的概率.14.甲和乙两个箱子中各装有10个球,其中甲箱中有5个红球、5个白球,乙箱中有8个红球、2个白球掷一枚质地均匀的骰子,如果点数为1或2,从甲箱子随机摸出1个球;如果点数为3,4,5,6,从乙箱子中随机摸出1个球求摸到红球的概率15.袋中有4个红球,3个黑球,这些球除颜色外完全相同,从袋中随机抽取球,设取到一个红球得2分,取到一个黑球得1分,从袋中任取4个球(1)求得分X的分布列;(2)求得分大于6分的概率16.2021年5月12日,2022北京冬奥会和冬残奥会吉祥物冰墩墩、雪容融亮相上海展览中心为了庆祝吉祥物在上海的亮相,某商场举办了一场赢取吉祥物挂件的“双人对战”游戏,游戏规则如下:参与对战的双方每次从装有3个白球和2个黑球(这5个球的大小、质量均相同,仅颜色不同)的盒子中轮流不放回地摸出1球,摸到最后1个黑球或能判断出哪一方获得最后1个黑球时游戏结束,得到最后1个黑球的一方获胜设游戏结束时对战双方摸球的总次数为X(1)求随机变量X的概率分布;(2)求先摸球的一方获胜的概率,并判断这场游戏是否公平17.(2022全国高二单元测试)溺水校园欺凌等与学生安全有关的问题越来越受到社会的关注和重视,为了普及安全教育,某市组织了一次学生安全知识竞赛,规定每队3人,每人回答一个问题,答对得1分,答错得0分.在竞赛中,甲乙两个中学代表队相遇,假设甲队3人回答正确的概率均为,乙队3人回答正确的概率分别为,且两队各人回答问题正确与否互不影响.(1)求甲队总得分为2分且乙队总得分为1分的概率;(2)求甲队总得分X的分布列和数学期望.18.9粒种子分别种在三个坑内,每坑3粒,每粒种子发芽的概率为05若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没有发芽,则这个坑需要补种,假定每个坑至多补种一次(1)求某个坑补种次数的数学期望与方差;(2)每补种一个坑需10元,用表示补种费用,写出的分布列,并求出的数学期望与方差选择性必修第三册 随机变量及其分布基础回归扎实练一、选择题1.(2021全国高二课时练习)设随机变量的正态分布密度函数为,则参数,的值分别是()A,B,C,D,【答案】D【解析】【分析】由正态分布密度函数的概念即得.【详解】由正态分布密度函数表达式知,.故选:D.2.已知,则等于( )ABCD【答案】C【分析】根据条件概率公式计算【详解】由,可得.故选:C.3.有一批种子的发芽率为0.9,出芽后的幼苗成活率为0.8,在这批种子中,随机抽取一粒,则这粒种子能成长为幼苗的概率是()A0.72B0.8C D0.9【答案】A【解析】【分析】设一批种子的发芽率为事件,则,出芽后的幼苗成活率为事件B,则,根据条件概率公式计算即可,【详解】设一批种子的发芽率为事件,则,出芽后的幼苗成活率为事件,则,这粒种子能成长为幼苗的概率.故选:A【点睛】本题主要考查了条件概率的问题,关键是分清是在什么条件下发生的,属于基础题4.若在一次测量中出现正误差和负误差的概率都是,则在5次测量中恰好出现2次正误差的概率是()A. B.C. D.【答案】 A【解析】PC23.5. 袋中装有大小相同的5个球,分别标有1,2,3,4,5五个号码,现在在有放回的条件下依次取出两个球,设两个球的号码之和为随机变量,则所有可能取值的个数是()A25B10C15D9【答案】D【解析】由题意得:两个球的号码之和可能为2,3,4,5,6,7,8,9,10,共9个.故选:D6.一袋中装有10个球,其中3个黑球、7个白球,从中先后随意各取一球(不放回),则第二次取到的是黑球的概率为()ABCD【答案】C【解析】【分析】明确第二次取到黑球分两类情况,结合全概率公式求解即可.【详解】记事件A,B分别表示第一、二次取到的是黑球,则,由题设易知P(A),P(B|A),于是P(B).故选:C7.若随机变量的分布列如下表所示,则的值为()1230.2A0.1B0.2C0.3D0.42【答案】B【解析】由题意得,解得,故选:B8.(2022全国模拟预测)同时抛掷两枚质地均匀的硬币一次,若两枚硬币都正面向上,就说这次试验成功,则3次试验中至少有2次成功的概率是()ABCD【答案】B【解析】【分析】先求出一次试验中两枚硬币都正面向上的概率,进而根据独立重复试验求概率的方法求得答案.【详解】在一次试验中,两枚硬币都正面向上的概率为,设X为3次试验中成功的次数,则,故所求概率.故选:B.二、填空题9.若,则_【答案】【分析】由条件概率公式直接计算得到结果.【详解】.故答案为:.10.设随机变量X的分布列,则常数a的值为_;_【答案】 .【解析】解题思路由题意得随机变量X的分布列为X1Pa2a3a4a5a由分布列的性质得,解得,;故答案为: .11.(2022吉林东北师大附中高二期末)某n重伯努利试验中,事件A发生的概率为p,事件A发生的次数记为X,则_【答案】【解析】【分析】根据二项分布的均值和方差的计算公式可求解【详解】依题意得X服从二项分布,则,解得,故答案为:12.某人外出出差,委托邻居给家里植物浇一次水,设不浇水,植物枯萎的概率为0.8,浇水,植物枯萎的概率为0.15邻居记得浇水的概率为0.9则该人回来植物没有枯萎的概率为_【答案】0.785【解析】【分析】根据题意,结合条件概率计算公式,即可求解.【详解】记A为事件“植物没有枯萎”,W为事件“邻居记得给植物浇水”,则根据题意,知,因此故答案为:0.785三、解答题13.已知一个不透明的口袋中有4个白球和8个红球,球除颜色外完全相同.(1)若一个人从口袋中随机抽取一个球,求其抽取到白球的概率;(2)若一个人从口袋中随机不放回连续抽取球两次,每次抽取一个球,求在第一次抽取出白球的条件下第二次抽取出的也是白球的概率.【答案】(1);(2).【解析】【分析】(1)利用古典概型的概率计算得解;(2)先计算出,再利用条件概率计算得解.【详解】(1)从口袋中随机抽取一个球,抽取到白球的概率.(2)记“第一次抽取出球是白球”为事件,“第二次抽取出球是白球”为事件,则第一次抽取出白球和第二次抽取出球也是白球的概率,,所以在第一次取出白球的条件下第二次取出的也是白球的概率.【点睛】本题主要考查古典概型的概率的计算,考查条件概率的计算,意在考查学生对这些知识的理解掌握水平.14.甲和乙两个箱子中各装有10个球,其中甲箱中有5个红球、5个白球,乙箱中有8个红球、2个白球掷一枚质地均匀的骰子,如果点数为1或2,从甲箱子随机摸出1个球;如果点数为3,4,5,6,从乙箱子中随机摸出1个球求摸到红球的概率【答案】【解析】设事件A为“掷一枚质地均匀的骰子,点数为1或2”,则事件为“掷一枚质地均匀的骰子,点数为3,4,5,6”;设事件B为“摸到红球”【点拨】全概率也是条件概率.15.袋中有4个红球,3个黑球,这些球除颜色外完全相同,从袋中随机抽取球,设取到一个红球得2分,取到一个黑球得1分,从袋中任取4个球(1)求得分X的分布列;(2)求得分大于6分的概率【答案】(1)X5678P(2)【解析】 (1)从袋中任取4个球的情况为1红3黑,2红2黑,3红1黑,4红,共四种情况,得分分别为5分,6分,7分,8分,故X的可能取值为5,6,7,8.P(X5),P(X6),P(X7),P(X8).故所求分布列为X5678P(2)根据随机变量的分布列可以得到大于6分的概率为P(X6)P(X7)P(X8).16.2021年5月12日,2022北京冬奥会和冬残奥会吉祥物冰墩墩、雪容融亮相上海展览中心为了庆祝吉祥物在上海的亮相,某商场举办了一场赢取吉祥物挂件的“双人对战”游戏,游戏规则如下:参与对战的双方每次从装有3个白球和2个黑球(这5个球的大小、质量均相同,仅颜色不同)的盒子中轮流不放回地摸出1球,摸到最后1个黑球或能判断出哪一方获得最后1个黑球时游戏结束,得到最后1个黑球的一方获胜设游戏结束时对战双方摸球的总次数为X(1)求随机变量X的概率分布;(2)求先摸球的一方获胜的概率,并判断这场游戏是否公平【答案】(1)X的分布列
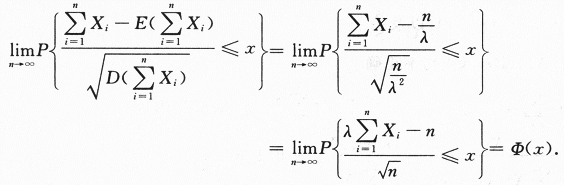
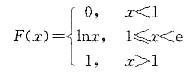 则X的概率密度函数f(x)为( )。
则X的概率密度函数f(x)为( )。 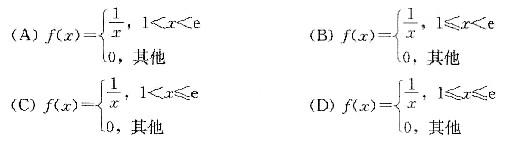
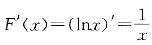 ,X的概率密度综合表示为
,X的概率密度综合表示为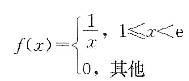
 则X的概率密度函数f(x)为( )。
则X的概率密度函数f(x)为( )。 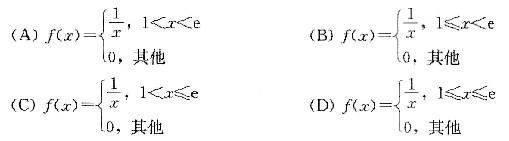
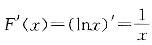 ,X的概率密度综合表示为
,X的概率密度综合表示为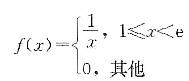

则数学期望E(X)等于( )。


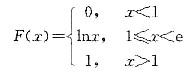 则X的概率密度函数f(x)为( )。
则X的概率密度函数f(x)为( )。 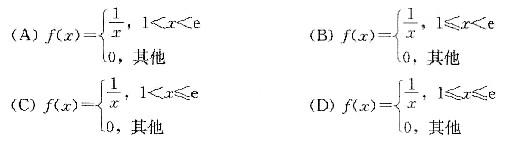
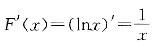 ,X的概率密度综合表示为
,X的概率密度综合表示为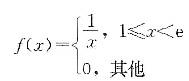
更多 “高二下学期数学人教A版(2019)选择性必修第三册第七章 随机变量及其分布 基础回归扎实练(word版 有答案)” 相关考题
- 根管充填应达到的标准为()。A、超填B、恰填C、糊剂超填D、牙胶尖欠填E、欠填
- 单选题下列哪个证件不属于实名证件的范围()A 临时身份证B 一代身份证C 二代身份证
- 发生颌骨放射性骨坏死的临界放射剂量指标为()A、30~50GyB、60~80GyC、90~10GyD、120~140GyE、100Gy
- 下列均属酰胺类局麻药的是()。A、普鲁卡因、利多卡因、丁卡因B、普鲁卡因、布比卡因、丁卡因C、普鲁卡因、罗哌卡因、丁卡因D、利多卡因、布比卡因、罗哌卡因E、利多卡因、布比卡因、丁卡因
- 男,体重60kg,烧伤总面积60%,Ⅲ度烧伤30%,伤后2周按照Curreri公式计算,每日需补充热卡()A、2900kcalB、3100kcalC、5500kcalD、3900kcalE、4900kcal
- 单选题普通客户借记卡账户挂失手续费()元A 15B 10C 20D 30
- 单选题工程师在确有必在时可以书面形式要求承包方停施工,但工程师应当在提出暂停施工要求后( )内提出书面处理意见。A 1天B 2天C 7天D 14天
- 单选题接电话时应在电话铃声()声内拿起话筒A 一B 二C 三D 四
- 多选题下述情况属于严禁办理的现钞存取款业务的有哪几项?()A我*行NRA人民币账户向他行境内单位或个人人民币账户发生资金收付B5个以上个人同一日内,共同在同一银行网点,每人办理接近等值5000美元的现钞结汇C其他通过多人次、多频次规避限额管理的分拆行为
- 关于整复手术的技术特点,以下叙述不正确的是()A、严格无菌条件B、尽量使用钝性分离C、爱护和保存组织D、防止或减少粗大瘢痕E、应用显微外科技术
- 浙江嘉兴南湖实验室招考聘用工作人员公告模拟题(带答案)_
- 浙江嘉兴市南湖区发展和改革局招考聘用编外用工公告强化练习题(带答案)_
- 浙江金华市医保基金第三方监管中心驻东工作人员招考聘用强化练习卷(带答案)_
- 浙江丽水龙泉市水利局招考聘用编外用工模拟题(带答案)_
- 浙江宁波北仑区社会矛盾纠纷调处化解中心选聘事业编制工作人员公告冲刺题(带答案)_
- 内蒙古兴安盟科右前旗农牧业事业单位引进高层次和急需紧缺人才公告强化练习卷(带答案)_
- 浙江宁波宁海县委老干部局招考聘用编外用工公告强化练习题(带答案)_
- 浙江宁波市鄞州区公立学校招考聘用编外员工公告冲刺卷(带答案)_
- 浙江宁波镇海区九龙湖镇招考聘用工作人员事宜冲刺卷(带答案)_
- 山东菏泽市第三人民医院招考聘用公告模拟题(带答案)_