2019本科《离散数学》期末试题及答案

网友您好，请在下方输入框内输入要搜索的题目：

2019本科《离散数学》期末试题及答案

下列关于关系模式规范化的叙述中，哪一条是不正确的？

A．若R∈BCNF，则必然R∈4NF

B．若R∈BCNF，则必然R∈3NF

C．若R∈BCNF，则必然R∈2NF

D．若R∈BCNF，则必然R∈1NF

正确答案：A

（54）下列关于关系模式规范化的叙述中，哪一条是不正确的？

A）若 R ? 4NF，则必然 R ? 3NF

B）若 R ? 3NF，则必然 R ? 2NF

C）若 R ? 2NF，则必然 R ? 1NF

D）若 R ? 1NF，则必然 R ? BCNF

正确答案：D

（54）【答案】D)
【解析】关系数据库中的关系必须满足一定的要求，即满足不同的范式。目前关系数据库有六种范式：第一范式（INF）、第二范式（2NF）、第三范式（3NF）、第四范式（4NF）、第五范式（5NF）和第六范式（6NF）。满足最低要求的范式是第一范式（1NF）。在第一范式的基础上进一步满足更多要求的称为第二范式（2NF），其余范式依次类推。一般来说，数据库只需满足第三范式（3NF）就行了。

设集合A={a,b,c},A上的二元关系R={,,}。下面命题中为假的是A.R不是偏序关系B.R是

设集合A={a,b,c},A上的二元关系R={＜a,a＞,＜b,b＞,＜c,c＞}。下面命题中为假的是

A．R不是偏序关系

B．R是等价关系

C．R是对称的

D．R是反对称的

正确答案：A

设集合A={a,b,c}，A上的二元关系R={, c,c>}，下面命题中为的是

A．R是对称的

B．R是反对称的

C．R是等价关系

D．R不是偏序关系

正确答案：D

设R，S是集合A上的二元关系，则下面命题是真命题的是

A．若R，S是自反的，则R?S是自反的

B．若R，S是反自反的，则R?S是反自反的

C．若R，S是对称的，则R?S是对称的

D．若R，S是传递的，则R?S是传递的

正确答案：A

2019本科离散数学期末试题及答案(试卷号1009)一、单项选择题(每小题3分，本题共15分)1. 若集合A=1.2,3,4).|MF列表述不正确的是()A. lAB. 】2.3)UAC. (1.2,3EAD. 0UA2. 若R,和R,是A上的对称关系，则中对称关系有(个A. 1R 2C. 3D. 43. 设G为连通无向图，则()时右中存在欧拉回路.A. G不存在奇数度数的结点B.G存在偶数度数的结点C. G存在一个奇数度数的结点D.G存在两个奇数度数的结点4. 无向图G是棵树.边敷是10,则G的结点度数之和是(.A. 20B.9a 10D.115. 设个体域为整数集，则公式Vx3y(x+=0)的解释可为()A. 存在一整数工有整数丫漕足工+=0B. 对任意整数工存在整数y满足言+=0C. 存在一整数对任息整数y满足x+=0D. 任意整数工对任意整数滴足丁+ =。得分评卷人二、填空题(每小H 3分.本共15分)6.设集合A =(1.2,3B = (2.3,4).C=(3.4.5).！WAU(C-B等于7. 设.4 = 2,3).8 = (I,2)C=(3.4).从 A 到 B 的函数/= .),从 B 到C 的SStg = (l,则 Dom上的关系：R = (VI,2V2.3V3,4,S=.试计算(1R Si.16. ffl G-，X中 VTjAcd（撬）,01皿（）,（6:）,脆）3）国应边的权值依次为2.33,5.6及7.试!）出 G 的fflJBi（2）写出G的邻投炖降（3）求出G权最小的生成村及其权值.17. 求P-（QAR）的析取液式与主合取范式.得分评卷人六、旺明（本共8分）18. 成址明日 n (P-*Q) An R A(Q P.试题答案及评分标准仅供参考一,项选择（每小BI3分,本题共15分）4. A5. Bl.C2.D3. A二q空（密小ii3分.本bi共15分） .6. （1.2.3,57. （2.3）（或人）8. 10 9.1 10.假（戒F 或0三、H辑公式*（小6分.本I共12分）IL tftP.学生的主璧任务是学习.则命题公式为，P12. 设今天天晞.Q,昨天下雨则命M公式为iPAQ四、判断说明（每小 7分,拿II共U分）13. 倍俱.空集的#集不为空集，为（0）.U.WW.完全IHK星平囱图.（2分）6分）（2分）6分）3分）（7分）（3分）（5分）（7分如K.可以如K图示岐入平囱.（4分）（8分）（12 分）五、计算（.h（2）RT = （V2.1V4.3QnS）= （,V2,2V3,3,V4.4）16. 解：（1G的图形表示为a3分）（6分）（2）邻接矩阵* 0 1 1 r 10 111（3）租线与站点点示的星小生成柳（10 分）权值为9A(n PVR)仃分)商i PVQ)V(A A)AVR)(7 分FVQ)V(R AA(VR)V(QAi Q)9 分)c4(n P VQVR) A( VQVA( VR VQ) A( VkVr Q)I 分)J /JVQVR)A(nPVQVnK)A(-iPVnQV/e) 主合取范式(】2 分六、证明JS（本共8分）18. 证明8(1)-1 n (P-Q)P（1分PQT(1)E（3分）Qf R)P3分(4H RP（5分）5)i Qr(3)(4)/（6分(6)-i PT(2)(5)I（8分）E（】因证明过程中.公式引用的次序可以不同一般引用前提正确得1分.利用两个公式得出有效结论得1或2分虽后得出结论得2或1分.（2）另可以用真值表验证.

下列关于关系模式规范化的叙述中，哪一条是不正确的？

A．若R∈BCNF，则必然R∈4NF

B．若R∈BCNF，则必然R∈3NF

C．若R∈BCNF，则必然R∈2NF

D．若R∈BCNF，则必然R∈1NF

正确答案：A
解析：

设集合{1234},A上的关系R={(12)(23)(24)(14)(34)}则R具有()

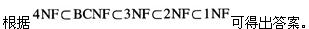
A、反自反性

B、传递性

C、对称性

D、以上答案都不对

参考答案：A

设集合A={1,2,3,4,5}上的关系R={x,y|x,yA且x+y=6}，则R的性质是()

A、自反的

B、对称的

C、对称的、传递的

D、反自反的、传递的

参考答案：B

设R是集合A上的二元关系,若R是传递的,则r(R)也是传递的,而s(R)不一定是传递的。()

此题为判断题(对，错)。

参考答案：正确

若集合A={1,2,3}上的二元关系R={<1,1>,<2,2>,<1,2>},则R是自反的关系。()

此题为判断题(对，错)。

参考答案：正确

网友您好， 请在下方输入框内输入要搜索的题目：

更多 “2019本科《离散数学》期末试题及答案” 相关考题

网友您好，请在下方输入框内输入要搜索的题目：