网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
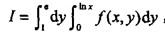,交换积分次序得()[其中f(x,y)是连续函数]。

参考答案

参考解析
解析：提示：画出积分区域图形，将该区域看成Y型区域。
更多 “,交换积分次序得()[其中f(x,y)是连续函数]。 ” 相关考题
考题 计算二重积分，其中D是由直线y=x,x=1以及x轴所围的区域.
查看答案
考题 设P(x,y,z),Q(x;y,z),R(x,y,z)是连续函数,M是在(S)上的最大值，其中(S)是一光滑曲面,其面积记为S.证明
查看答案
考题 设f(x)为连续函数，且下列极限都存在，则其中可推出f′(3)存在的是( )。A. B. C. D.
查看答案
考题 下列( )项是在D={(x，y)|x2+y2≤1，x≥0，y≥0)上的连续函数f(x，y)，且f(x，y)=3(x+y)+16xy。 A.f(x，y)=3(x+y)+32xy B.f(x，y)=3(x+y)-32xy C.f(x，y)=3(x+y)-16xy D.f(x，y)=3(x+y)+16xy
查看答案
考题 设f（x）、f'（x）为已知的连续函数，则微分方程y'+ f'（x）y = f（x）f'（x）的通解是：
查看答案
考题 设f(x),f'(x)为已知的连续函数，则微分方程y'十f'(x)y=f(x)f'(x)的通解是： A. y=f(x)+ce-f(x) B. y= f(x)ef(x) -ef(x) +c C. y=f(x)-1+ce-f(x) D. y=f(x)-1+cef(x)
查看答案
考题 D 域由 x 轴，x2 + y2 ? 2x = 0( y ≥ 0)及 x+y=2 所围成， f (x, y)是连续函数，化
查看答案
考题 设二重积分，交换积分次序后，则I等于：
查看答案
考题 交换二次积分的积分次序：
查看答案
考题 计算二重积分，其中积分区域D是由x=0、x=1、y=0、y=1所围成的闭区域
查看答案
考题 设f(x，y)为连续函数，且满足，其中D是由x轴、y轴、所围成的闭区域
查看答案
考题 已知微分方程y’+y=f(x)，其中f(x)是R上的连续函数. 　　(Ⅰ)若f(x)=x，求方程的通解. 　　(Ⅱ)若f(x)是周期为T的函数，证明：方程存在唯一的以T为周期的解.
查看答案
考题 已知函数f(x，y)具有二阶连续偏导数，且，其中D={(x，y)｜0≤x≤1，0≤y≤1)，计算二重积分.
查看答案
考题 设f（x，y）为连续函数，则等于：
查看答案
考题 非负连续函数f(x)满足f(0)=0,f(1)=1.已知以曲线y=f(x)为曲边，以[0,x]为底的曲边梯形，其面积与f(x)的n+1次幂成正比，则f(x)的表达式为
查看答案
考题 设连续函数f（x）满足方程
查看答案
考题 设f（x）为区间[a，b]上的连续函数，则曲线y=f（x）与直线x=a，x=b，y=0所围成的封闭图形的面积为（ ）.《》（ ）
查看答案
考题 如图，连续函数y＝f(x)在区间[一3，一2]，[2，3]上的图形分别是直径为l的上、下半圆周，
查看答案
考题 设f(x，y)为连续函数，
查看答案
考题 (1)求曲线y=f(x)； (2)求由曲线y=f(x)，y=0，x=1所围图形绕x轴旋转一周所得旋转体体积．
查看答案
考题 若连续函数y=f（x）在x0点不可导，则曲线y=f(x)在（x0,f(x0））点没有切线.
查看答案
考题 随机变量的X分布函数F（X）是右连续函数。
查看答案
考题 填空题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。
查看答案
考题 单选题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。A 1B －1C 1/7D －1/7
查看答案
考题 填空题设z＝f（xy，x/y）＋g（y/x），其中f、g均可微，则∂z/∂x＝____。
查看答案
考题 判断题若连续函数y=f（x）在x0点不可导，则曲线y=f(x)在（x0,f(x0））点没有切线.A 对B 错
查看答案
考题 填空题设f（x，y）＝ax＋by，其中a，b为常数，则f[xy，f（x，y）]＝____。
查看答案
热门标签
最新试卷