考题
设（X，Y）服从在区域D上的均匀分布，其中D为x轴、y轴及x+y=1所围成，求X与Y的协方差Cov(X,Y).
考题
设平面区域D由曲线y=1／x及直线y=0,x=1,x=е2所围成,二维随机变量(X,Y)在区域D上服从均匀分布,则(X,Y)的联合密度函数为()。
考题
计算二重积分，其中D是由直线y=x,x=1以及x轴所围的区域.
考题
若D是由x轴、y轴及直线2x＋y－2＝0所围成的闭区域，则二重积分
的值等于（ ）A．1
B．2
C．1/2
D．－1
考题
D是由y2=x及y=x-2所围成的区域，则化为二次积分后的结果为：
考题
Ω是由曲面z=x2+y2，y=x，y=0，z=1在第一卦限所围成的闭区域，f（x，y，z） 在Ω上连续，则等于：
考题
设D是曲线y=x2与y=1所围闭区域，等于：
(A)1 (B) (C)0 (D)2
考题
若D是由x=0，y=0，x2+y2=1所围成在第一象限的区域，则二重积分
等于（ ）。
考题
设平面闭区域D由x=0，y=0，x+y=1/2，x+y=1 所围成。
A.I123 B. I132
C. I321 D. I312
考题
D域由x轴、x2+y2-2x=0(y≥0)及x+y=2 所围成，f(x,y)是连续函
考题
D是由y2=x及y=x-1所围成的区域，则化为二次积分后的结果为:
考题
设D是由直线y=1，y=x，y=-x围成的有界区域，计算二重积分
考题
设f(x，y)为连续函数，且满足，其中D是由x轴、y轴、所围成的闭区域
考题
请计算，其中D是由y=1/x=2,y=x所围成的闭区域
考题
请计算二重积分，其中D是由圆周、x轴，y轴所围成的在第一象限内的闭区域
考题
设二维随机变量(X，Y)服从区域G上的均匀分布，其中G是由x-y=0，x+y=2，与y=0所围成的三角形区域.
(Ⅰ)求X的概率密度fx(x)；
(Ⅱ)求条件概率密度.
考题
已知函数f(x，y)具有二阶连续偏导数，且，其中D={(x，y)｜0≤x≤1，0≤y≤1)，计算二重积分.
考题
D域由x轴、x2+y2-2x=0(y≥0)及x+y=2 所围成，f(x,y)是连续
考题
设平面闭区域D由x=0，y=0，x+y=1/2，x+y=1 所围成。
A.I123
B. I132
C. I321
D. I312
考题
(1)求f(x)和g(x)围成的平面区域的面积.?
(2)求0≤y≤f(x), 1≤x≤3,绕y轴旋转的体积.?
考题
设区域D是由直线y=x，x=2，y=1围成的封闭平面图形，
考题
，其中区域如图5-3所示，由y=x，y=1与Y轴围成．
考题
计算二重积分
，其中D是由直线
及y=1围
成的平面区域．
考题
设二维随机变量（X，Y）在区域D上服从均匀分布，其中D://0≤x≤2，0≤y≤2。记（X，Y）的概率密度为f（x，y），则f（1，1）=（）
考题
被积函数f（x，y）在被积区域D上的二重积分的几何意义是：在区域D上曲面z=f（x，y）所围曲顶体的体积。
考题
问答题(X,Y)服从矩形区域D={(x，y)| 0≤X≤2，0≤y≤2}上的均匀分布，则P{0≤X≤1,1≤Y≤2}=_____
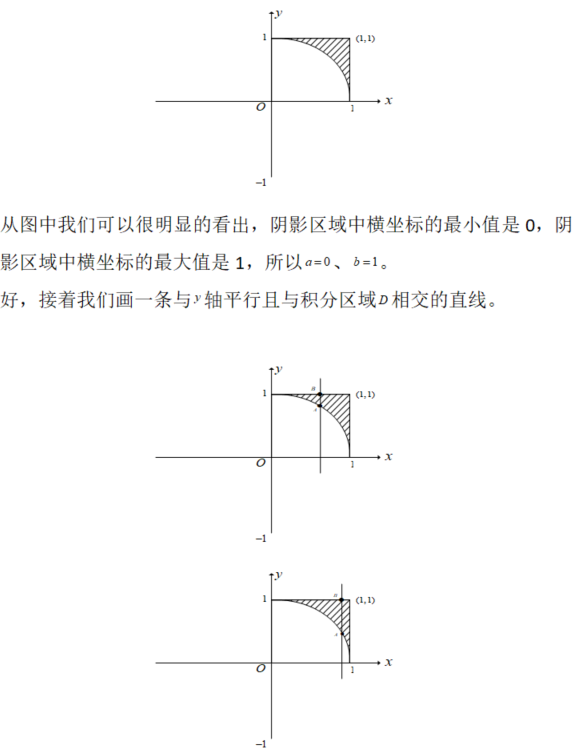
，其中积分区域D是由x=0、x=1、y=0、y=1所围成的闭区域
