网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
图G的邻接矩阵如下图所示(顶点依次表示为v0、v1、v2、v3、v4、v5),G是( )。对G进行广度优先遍历(从v0开始),可能的遍历序列为(请作答此空)。


A.v0、v1、v2、v3、v4、v5
B.v0、v2、v4、 v5、v1、v3
C.v0、v1、v3、v5、v2、v4
D.v0、v2、v4、v3、v5、v1
B.v0、v2、v4、 v5、v1、v3
C.v0、v1、v3、v5、v2、v4
D.v0、v2、v4、v3、v5、v1
参考答案
参考解析
解析: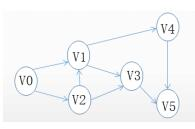

更多 “ 图G的邻接矩阵如下图所示(顶点依次表示为v0、v1、v2、v3、v4、v5),G是( )。对G进行广度优先遍历(从v0开始),可能的遍历序列为(请作答此空)。 A.v0、v1、v2、v3、v4、v5 B.v0、v2、v4、 v5、v1、v3 C.v0、v1、v3、v5、v2、v4 D.v0、v2、v4、v3、v5、v1 ” 相关考题
考题
已知有向图G=(V,E),其中V={V1,V2,V3,V4, V5,V6},E={<V1,V2>,<V1,V4>,<V2,V6>,<V3,V1>, <V3,V4>,<V4,V5>,<V5,V2>,<V5,V6>},G的拓扑序列是(50)。A.V3,V1,V4,V5,V2,V6B.V3,V4,V1,V5,V2,V6C.V1,V3,V4,V5,V2,V6D.V1,V4,V3,V5,V2,V6
考题
已知某图的邻接表如图4-12所示。①此邻接表所对应的无向图为(14)。②此图由F开始的深度优先遍历为(15)。③此图由9开始的深度优先遍历的支撑树为(16)。④此图由F开始的广度优先遍历为(17)。⑤此图由9开始的广度优先遍历的支撑树为(18)。A.B.C.
考题
设有向图G=(V,E),其中V={V1,V2,V3,V4,V5,V6,V7,V8),E={V1,V2>,<V1,V3>,<V2,V4>,<V2,V6>,<V3,V5>,<V4,V8>,<V5,V4>,<V6,V3>,<V6,V7>, (V7,V5>,<V8,V7>),那么该图的邻接表可以是(10),按照该邻接表从V1,出发,图G的深度优先遍历序列为(11),广度优先遍历序列为(12)。A.B.C.D.
考题
已知无向图的邻接表如图2-35所示。此邻接表对应的无向图为(1)。此图从F开始的深度优先遍历为(2)。从F开始的广度优先遍历为(3)。从F开始的深度优先生成树为 (4)。从F开始的广度优先生成树为(5)。A.B.C.
考题
图2-36是带权的有向图G的邻接表。以结点V1出发深度遍历图G所得的结点序列为(1);广度遍历图G所得的结点序列为(2);G的一种拓扑序列是(3);从结点V1到V8结点的最短路径是(4);从结点V1到V8结点的关键路径是(5)。A.V1,V2,V3,V4,V5,V6,V7,V8B.V1,V2,V3,V8,V4,V5,V6,V7C.V1,V2,V3,V8,V4,V5,V7,V6D.V1,V2,V3,V8,V5,V7,V4,V6
考题
设无向图G=(P,L),P={v1,v2,v3,v4,v5,v6},L={(v1,v2),(v2,v2),(v2,v4),(v4,v5),(v3,v4),(v1,v3),(v3,v1)}。G中奇数度顶点的个数是(60)。A.2B.3C.4D.5
考题
阅读以下说明和代码,填补代码中的空缺,将解答填入答题纸的对应栏内。 【说明】 图是很多领域中的数据模型,遍历是图的一种基本运算。从图中某顶点v出发进行广度优先遍历的过程是: ①访问顶点v; ②访问V的所有未被访问的邻接顶点W1 ,W2 ,..,Wk; ③依次从这些邻接顶点W1 ,W2 ,..,Wk出发,访问其所有未被访问的邻接顶点;依此类推,直到图中所有访问过的顶点的邻接顶点都得到访问。 显然,上述过程可以访问到从顶点V出发且有路径可达的所有顶点。对于从v出发不可达的顶点u,可从顶点u出发再次重复以上过程,直到图中所有顶点都被访问到。 例如,对于图4-1所示的有向图G,从a出发进行广度优先遍历,访问顶点的一种顺序为a、b、c、e、f、d。设图G采用数组表示法(即用邻接矩阵arcs存储),元素arcs[i][j]定义如下:图4-1的邻接矩阵如图4-2所示,顶点a~f对应的编号依次为0~5.因此,访问顶点a的邻接顶点的顺序为b,c,e。 函数BFSTraverse(Graph G)利用队列实现图G的广度优先遍历。 相关的符号和类型定义如下: define MaxN 50 /*图中最多顶点数*/ typedef int AdjMatrix[MaxN][MaxN]; typedef struct{ int vexnum, edgenum; /*图中实际顶点数和边(弧)数*/ AdjMatrix arcs; /*邻接矩阵*/ )Graph; typedef int QElemType; enum {ERROR=0;OK=1}; 代码中用到的队列运算的函数原型如表4-1所述,队列类型名为QUEUE。 表4-1 实现队列运算的函数原型及说明【代码】 int BFSTraverse(Graph G) {//对图G进行广度优先遍历,图采用邻接矩阵存储 unsigned char*visited; //visited[]用于存储图G中各顶点的访问标志,0表示未访问 int v, w, u; QUEUEQ Q; ∥申请存储顶点访问标志的空间,成功时将所申请空间初始化为0 visited=(char*)calloc(G.vexnum, sizeof(char)); If( (1) ) retum ERROR; (2) ; //初始化Q为空队列 for( v=0; vG.vexnum; v++){ if(!visited[v]){ //从顶点v出发进行广度优先遍历 printf(%d,v); //访问顶点v并将其加入队列 visited[v]=1; (3) ; while(!isEmpty(Q)){ (4) ; //出队列并用u表示出队的元素 for(w=0;vG.vexnum; w++){ if(G.arcs[u][w]!=0 (5) ){ //w是u的邻接顶点且未访问过 printf(%d, w); //访问顶点w visited[w]=1; EnQueue(Q, w); } } } } free(visited); return OK; )//BFSTraverse
考题
对于下图,从顶点l进行深度优先遍历时,不可能得到的遍历序列是(42);若将该图用邻接矩阵存储,则矩阵中的非0元素数目为(43)。A.1234567B.1523467C.1234675D.1267435
考题
试题四(共 15 分)阅读以下说明和代码,填补代码中的空缺,将解答填入答题纸的对应栏内。【说明】 图是很多领域中的数据模型,遍历是图的一种基本运算。从图中某顶点 v出发进行广度优先遍历的过程是:①访问顶点 v;②访问 V 的所有未被访问的邻接顶点 W1 ,W2 ,..,Wk;③依次从这些邻接顶点 W1 ,W2 ,..,Wk 出发,访问其所有未被访问的邻接顶 点;依此类推,直到图中所有访问过的顶点的邻接顶点都得到访问。显然,上述过程可以访问到从顶点 V 出发且有路径可达的所有顶点。对于 从 v 出发不可达的顶点 u,可从顶点 u 出发再次重复以上过程,直到图中所有顶 点都被访问到。例如,对于图 4-1 所示的有向图 G,从 a 出发进行广度优先遍历,访问顶点 的一种顺序为 a、b、c、e、f、d。图 4-1
设图 G 采用数组表示法(即用邻接矩阵 arcs 存储),元素 arcs[i][ j]定义如下:
图 4-1 的邻接矩阵如图 4-2 所示,顶点 a~f 对应的编号依次为 0~5.因此,访问顶点 a 的邻接顶点的顺序为 b,c,e。函数 BFSTraverse(Graph G)利用队列实现图 G 的广度优先遍历。相关的符号和类型定义如下:#define MaxN:50 /*图中最多顶点数*/ typedef int AdjMatrix[MaxN][MaxN];typedef struct{int vexnum,edgenum;/*图中实际顶点数和边(弧)数*/ AdjMatrix arcs; /*邻接矩阵*/)Graph;typedef int QElemType; enum {ERROR=0;OK=l};代码中用到的队列运算的函数原型如表 4-1 所述,队列类型名为 QUEUE。
表 4-1 实现队列运算的函数原型及说明
【代码】int BFSTraverse(Graph G){//图 G 进行广度优先遍历,图采用邻接矩阵存储unsigned char*visited; //visited[]用于存储图 G 中各顶点的访问标 志,0 表示未访问int v,w;u;
QUEUEQ Q;∥申请存储顶点访问标志的空间,成功时将所申请空间初始化为 0 visited=(char*)calloc(G.vexnum, sizeof(char));If( (1) ) retum ERROR; (2) ; //初始化 Q 为空队列 for( v=0; v } free(visited);return OK;)//BFSTraverse从下列的 2 道试题(试题五至试题六)中任选 1 道解答。请在答题纸上的 指定位置处将所选择试题的题号框涂黑。若多涂或者未涂题号框,则对题号最小 的一道试题进行评分。
考题
对于下图,从顶点1进行深度优先遍历时,不可能得到的遍历序列是(请作答此空);若将该图用邻接矩阵存储,则矩阵中的非0元素数目为( )。
A.1234.567
B.1523467
C.1234675
D.1267435
考题
针对下图所示的有向图,从结点V1出发广度遍历所得结点序列和深度遍历所得结点序列分别是______。
A.V1,V2,V3,V4,V5,V6,V7,V8和V1,V2,V3,V8,V5,V7,V4,V6
B.V1,V2,V4,V6,V3,V5,V7,V8和V1,V2,V3,V8,V5,V7,V4,V6
C.V1,V2,V4,V6,V3,V5,V7,V8和V1,V2,V3,V8,V4,V5,V6,V7
D.V1,V2,V4,V6,V7,V3,V5,V8和V1,V2,V3,V8,V5,V7,V4,V6
考题
图G的邻接矩阵如下图所示(顶点依次表示为v0、v1、v2、v3、v4、v5),G是(请作答此空)。对G进行广度优先遍历(从v0开始),可能的遍历序列为( )。
A.无向图
B.有向图
C.完全图
D.强连通图
考题
阅读下列说明和?C?代码,回答问题?1?至问题?2,将解答写在答题纸的对应栏内。
【说明】
一个无向连通图?G?点上的哈密尔顿(Hamiltion)回路是指从图?G?上的某个顶点出发,经过图上所有其他顶点一次且仅一次,最后回到该顶点的路劲。一种求解无向图上哈密尔顿回
路算法的基础私下如下:假设图?G?存在一个从顶点?V0?出发的哈密尔顿回路?V1——V2——V3——...——Vn-1——V0。算法从顶点?V0?出发,访问该顶点的一个未被访问的邻接顶点?V1,接着从顶点?V1?出发,访问?V1?一个未被访问的邻接顶点?V2,..。;对顶点?Vi,重复进行以下操作:访问?Vi?的一个未被访问的邻接接点?Vi+1;若?Vi?的所有邻接顶点均已被访问,则返回到顶点?Vi-1,考虑Vi-1?的下一个未被访问的邻接顶点,仍记为?Vi;知道找到一条哈密尔顿回路或者找不到哈密尔顿回路,算法结束。
【C?代码】
下面是算法的?C?语言实现。
(1)常量和变量说明
n :图?G?中的顶点数
c[][]:图?G?的邻接矩阵
K:统计变量,当期已经访问的定点数为?k+1
x[k]:第?k?个访问的顶点编号,从?0?开始
Visited[x[k]]:第?k?个顶点的访问标志,0?表示未访问,1?表示已访问
⑵C?程序
【问题?1】(10?分)
根据题干说明。填充?C?代码中的空(1)~(5)。
【问题?2】(5?分)
根据题干说明和?C?代码,算法采用的设计策略为( ),该方法在遍历图的顶点时,采用的
是(?)方法(深度优先或广度优先)。
考题
已知有向图G=(V,E),其中V={V1,V2,V3,V4,V5,V6,V7},E={ V1,V2, V1,V3, V1,V4, V2,V5, V3,V5, V3,V6, V4,V6, V5,V7, V6,V7},G的拓扑序列是()。A、V1,V3,V4,V6,V2,V5,V7B、V1,V3,V2,V6,V4,V5,V7C、V1,V3,V4,V5,V2,V6,V7D、V1,V2,V5,V3,V4,V6,V7
考题
已知无向图G描述如下:
G=(V,E)
V={V1,V2,V3,V4,V5}
E={(V1,V2),(V1,V4),(V2,V4),(V3,V4),(V2,V5),(V3,V4),(V3,V5)}
写出每个顶点的度。
考题
问答题已知无向图G描述如下:
G=(V,E)
V={V1,V2,V3,V4,V5}
E={(V1,V2),(V1,V4),(V2,V4),(V3,V4),(V2,V5),(V3,V4),(V3,V5)}
写出每个顶点的度。
热门标签
最新试卷