网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
以“余弦定理”教学为例,简述数学定理数学的主要环节。
参考答案
参考解析
解析:(1)创设情境,提出问题
问题:以千岛湖求两岛间的距离引入,已知两岛间的距离及夹角如何求另两岛间的距离。
老师活动:以上问题能否用正弦定理来解决,请同学们深度一下,如果解决不了,思考它是已知三角形两边及夹角,求第三边的问题。能否也象正弦定理那样,寻找它们之间的某种定量关系?
(2)求异探新,证明定理
问题1:这是一个已知三角形两边a和b及两边的夹角C,求出第三边c的问题。我们知道已知三角形两边分别为a和b,这两边的夹角为C,角C满足什么条件时较易求出第三边c?(由勾股定理导入)
问题2:自学提纲
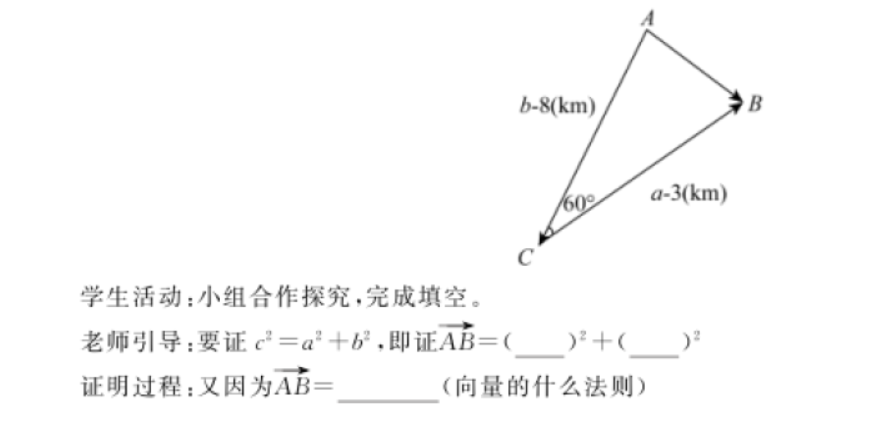

老师活动:引导学生从特殊入手,用已有的初中所学的平面几何的有关知识来研究这一问题,从而寻找出这些量之间存在的某种定量关系。得出结论,上式就是余弦定理。师生强调:得出了余弦定理,还应引导学生联想、类比、转化,思考是否还有其他方法证明余弦定理。
问题3:让学生观察以下各式的结构有什么特征?能用语言描述吗?
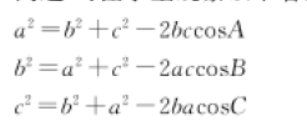
师生共同总结:余弦定理的内容是三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦的积的两倍。
(3)巩固新知,运用练习
询问学生这节课的收获,能否学以致用。请小组继续自学教材上的两个例题。比一比,赛一赛。看哪一个小组先发现这两个生活实际问题的解决能否用今天学的余弦定理?如何解决?
(4)运用定理,解决问题
让学生观察余弦定理及推论的构成形式,思考用余弦定理及推论可以解决那些类型的三角形问题。
定理学习的一般环节:
(1)了解定理的内容,能够解决什么问题(创设情境,提出问题中体现);(2)理解定理的含义,认识定理的条件和结论,如在公式推导过程中对条件引起注意,通过对结论从结构,功能,性质,使用步骤等角度分析以加深印象和理解(求异探新,证明定理中体现);(3)定理的证明或推导过程;学生与老师一起研究证明方法,如不需证明,学生根据老师提供的材料体会定理规定的合理性(求异探新,证明定理中体现);(4)熟悉定理的使用。循序渐进地定理的应用,将定理纳入到已有的知识体生系中去(巩固新知,运用练习中体现);(5)引申和拓展定理的运用(运用定理,解决问题中体现)。
问题:以千岛湖求两岛间的距离引入,已知两岛间的距离及夹角如何求另两岛间的距离。
老师活动:以上问题能否用正弦定理来解决,请同学们深度一下,如果解决不了,思考它是已知三角形两边及夹角,求第三边的问题。能否也象正弦定理那样,寻找它们之间的某种定量关系?
(2)求异探新,证明定理
问题1:这是一个已知三角形两边a和b及两边的夹角C,求出第三边c的问题。我们知道已知三角形两边分别为a和b,这两边的夹角为C,角C满足什么条件时较易求出第三边c?(由勾股定理导入)
问题2:自学提纲


老师活动:引导学生从特殊入手,用已有的初中所学的平面几何的有关知识来研究这一问题,从而寻找出这些量之间存在的某种定量关系。得出结论,上式就是余弦定理。师生强调:得出了余弦定理,还应引导学生联想、类比、转化,思考是否还有其他方法证明余弦定理。
问题3:让学生观察以下各式的结构有什么特征?能用语言描述吗?
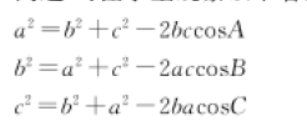
师生共同总结:余弦定理的内容是三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦的积的两倍。
(3)巩固新知,运用练习
询问学生这节课的收获,能否学以致用。请小组继续自学教材上的两个例题。比一比,赛一赛。看哪一个小组先发现这两个生活实际问题的解决能否用今天学的余弦定理?如何解决?
(4)运用定理,解决问题
让学生观察余弦定理及推论的构成形式,思考用余弦定理及推论可以解决那些类型的三角形问题。
定理学习的一般环节:
(1)了解定理的内容,能够解决什么问题(创设情境,提出问题中体现);(2)理解定理的含义,认识定理的条件和结论,如在公式推导过程中对条件引起注意,通过对结论从结构,功能,性质,使用步骤等角度分析以加深印象和理解(求异探新,证明定理中体现);(3)定理的证明或推导过程;学生与老师一起研究证明方法,如不需证明,学生根据老师提供的材料体会定理规定的合理性(求异探新,证明定理中体现);(4)熟悉定理的使用。循序渐进地定理的应用,将定理纳入到已有的知识体生系中去(巩固新知,运用练习中体现);(5)引申和拓展定理的运用(运用定理,解决问题中体现)。
更多 “以“余弦定理”教学为例,简述数学定理数学的主要环节。” 相关考题
考题
单选题1745年数学家()运用余弦定理推导出椭圆方程。A
洛必达B
约翰·伯努利C
斯蒂尔D
笛卡尔
热门标签
最新试卷