网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
已知向量a,b，满足|a|=|b|=1，且|a-kb|=√3|ka+b|，其中k>0。
(1)试用k表示a b，并求出a b的最大值及此时a与b的夹角θ的值：
(2)当a b取得最大值时，求实数A，使|a+λb|的值最小，并对这一结论作出几何解释。

参考答案

参考解析
解析：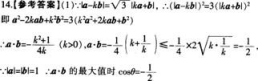
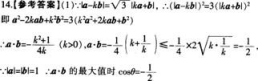
更多 “已知向量a,b，满足|a|=|b|=1，且|a-kb|=√3|ka+b|，其中k>0。 (1)试用k表示a b，并求出a b的最大值及此时a与b的夹角θ的值： (2)当a b取得最大值时，求实数A，使|a+λb|的值最小，并对这一结论作出几何解释。” 相关考题
考题 设向量x垂直于向量a=(2，3，-1)和b=(1，-2，3)且与c=(2，-1，1)的数量积为-6，则向量x=( )。A.(-3，3，3) B.(-3，1，1) C.(0，6，0) D.(0，3，-3)
查看答案
考题 A.过点(0，-2，1)，方向向量为2i-j-3k B.过点(0，-2，1)，方向向量为-2i-j+3k C.过点(0，2，-1)，方向向量为2i+j-3k D.过点(O，2，-1)，方向向量为-2i+j+3k
查看答案
考题 3维向量组A：a1，a2，…，am线性无关的充分必要条件是( ).A.对任意一组不全为0的数k1，k2，…，km，都有k1a1+k2a2+…+kmam≠0 B.向量组A中任意两个向量都线性无关 C.向量组A是正交向量组 D.
查看答案
考题 已知三维列向量αβ满足αTβ=3，设3阶矩阵A=βαT，则： A. β是A的属于特征值0的特征向量 B. α是A的属于特征值0的特征向量 C. β是A的属于特征值3的特征向量 D. α是A的属于特征值3的特征向量
查看答案
考题 向量组α1=(1，1，1，1)'，α2=(1，1，1，0)'，α3=(1，k，0，0)，α4=(1，0，0，0)线性无关，则( )。A、k≠0 B、k≠1 C、k≠2 D、k≠3
查看答案
考题 已知4元非齐次线性方程组Ax=b的系数矩阵的秩等于3，且η1，η2，η3是3个不同的解向量，则通解是( ).A.x=k1(η-η2)+η3 B.x=k1η1+k2η2+η3 C.x=k1η1+k2η2+k3η3 D.x=k1(η+η2)+η3
查看答案
考题 已知向量a、b、c都是单位向量，且满足a+b+c=0．则a·b+b·c+c·a=( )。
查看答案
考题 设λ1，λ2是矩阵A的2个不同的特征值，ξ，η是A的分别属于λ1，λ2的特征向量，则以下选项中正确的是： A. 对任意的k1≠0和k2≠0，k1ξ+k2η都是A的特征向量 B.存在常数k1≠0和k2≠0，使得k1ξ+k2η是A的特征向量 C.存在任意的k1≠0和k2≠0，k1ξ+k2η都不是A的特征向量 D.仅当k1=0和k2=0，k1ξ+k2η是A的特征向量
查看答案
考题 设λ1，λ2是矩阵A 的2 个不同的特征值，ξ，η 是A 的分别属于λ1，λ2的特征向量， 则以下选项中正确的是： （A）对任意的k1≠ 0和k2 ≠0，k1 ξ+k2η 都是A 的特征向量 （B）存在常数k1≠ 0和k2≠0，使得k1ξ+k2η 是A 的特征向量 （C）存在任意的k1≠ 0和k2≠ 0， k1ξ+ k2η 都不是A 的特征向量 （D）仅当k1=k2=时， k1ξ+k2 η 是A 的特征向量
查看答案
考题 设直线的方程为则直线： (A)过点(1,-1,0)，方向向量为2i + j-k (B)过点(1,-1,0)，方向向量为2i - j + k (C)过点(-1,1,0)，方向向量为-2i - j + k (D)过点(-1,1,0)，方向向量为2i + j - k
查看答案
考题 已知三维列向量a，β满足aTβ，设3阶矩阵A=βaT，则: A. β是A的属于特征值0的特征向量 B. a是A的属于特征值0的特征向量 C. β是A的属于特征值3的特征向量 D. a是A的属于特征值3的特征向量
查看答案
考题 已知向量a，b，满足 其中k>0。 (1)试用k表示a·b，并求出a·b的最大值及此时aL5 b的夹角0的值： (2)当a·b取得最大值时，求实数A，使la+Abl的值最小，并对这一结论作出几何解释。
查看答案
考题 已知向量a=(k，3)，b=(1，4)，c=(2，1)，R(2a一3b)上c，则实数k=( )。A.-4．5 B.0 C.3 D.5．5
查看答案
考题 已知3维列向量α，β满足αTβ=3，设3阶矩阵A=βαT，则（）。A、β是A的属于特征值0的特征向量B、α是A的属于特征值0的特征向量C、β是A的属于特征值3的特征向量D、α是A的属于特征值3的特征向量
查看答案
考题 设λ1，λ2是矩阵A的两个不同的特征值，ξ、η是a的分别属于λ1、λ2的特征向量，则以下选项正确的是（）。A、对任意的k1≠0和k2≠0，k1ξ+k2η都是A的特征向量B、存在常数k1≠0和k2≠0，使得k1ξ+k2η是A的特征向量C、对任意的k1≠0和k2≠0，k1ξ+k2η都不是A的特征向量D、仅当k1=k2=0时，k1ξ+k2η是A的特征向量
查看答案
考题 填空题已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1＋α(→)2＝（1，1，0，2）T，α(→)2＋α(→)3＝（l，0，1，3）T，则AX(→)＝b(→)的通解是____。
查看答案
考题 单选题已知3维列向量α，β满足αTβ=3，设3阶矩阵A=βαT，则（）。A β是A的属于特征值0的特征向量B α是A的属于特征值0的特征向量C β是A的属于特征值3的特征向量D α是A的属于特征值3的特征向量
查看答案
考题 问答题已知m个向量α(→)1，α(→)2，…，α(→)m线性相关，但其中任意m－1个都线性无关，证明：　　（1）如果存在等式k1α(→)1＋…＋kmα(→)m＝0(→)，则这些系数k1，…，km或者全为零，或者全不为零。　　（2）如果存在两个等式k1α(→)1＋…＋kmα(→)m＝0(→)，l1α(→)1＋…＋lmα(→)m＝0(→)，其中l1≠0，则k1/l1＝k2/l2＝…＝km/lm。
查看答案
考题 单选题设λ1，λ2是矩阵A的2个不同的特征值，ξ，η是A的分别属于λ1，λ2的特征向量，则以下选项中正确的是：（）A 对任意的k1≠0和k2≠0，k1ξ+k2η，都是A的特征向量B 存在常数k1≠0和k2≠0，使得k1ξ+k2η，是A的特征向量C 存在任意的k1≠0和k2≠0，k1ξ+k2η，都不是A的特征向量D 仅当k1=k2=0时，k1ξ+k2η，是A的特征向量
查看答案
考题 单选题设向量x垂直于向量a=（2，3，-1）和b=（1，-2，3），且与c=（2，-1，1）的数量积为-6，则向量x=（　　）。A （-3，3，3）B （-3，1，1）C （0，6，0）D （0，3，-3）
查看答案
热门标签
最新试卷