网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
过点(1,-2,3)且平行于z轴的直线的对称式方程是( )。


参考答案
参考解析
解析:由题意可得此直线的方向向量为(0,0,1),又过点(1,-2,3),所以该直线的方程为
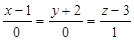
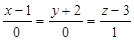
更多 “过点(1,-2,3)且平行于z轴的直线的对称式方程是( )。 ” 相关考题
考题
过点(0,2,4)且与两平面x+2z=1和y-3z=2平行的直线方程是( ).A.x/0=(y-2)/1=(z-4)/(-3)
B.x/1=(y-2)/0=(z-4)/2
C.x/(-2)=(y-2)/(-3)=(z-4)/1
D.x/(-2)=(y-2)/3=(z-4)/1
考题
在平面直角坐标系中,以坐标原点0为极点,x轴的正半轴为极轴建立极坐标系。已知 点A的极坐标为.直线Z的极坐标方程为且点A在直线Z上。
(1)求。的值及直线Z的直角坐标方程;
(2)圆C的参数方程为试判断直线Z与圆C的位置关系。
考题
过点(2,-3,1)且平行于向量a=(2,-1,3)和b=(-1,1,-2)的平面方程是( ).A.-x+y+z-4=0
B.x-y-z-4=0
C.x+y+z=0
D.x+y-z+2=0
考题
过点(4,-1,3)且平行于直线L:(x-3)/2=y=(z-1)/5的直线方程为( ).A.(x-4)/2=(y+1)/0=(z-3)/5
B.(x-4)/2=(y+1)/1=(z-3)/5
C.(x+4)/2=(y-1)/0=(z+3)/5
D.(x+4)/2=(y-1)/1=(z+3)/5
考题
已知中心在坐标原点0的椭圆C经过点A(2,3)且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线l,使l与椭圆C有公共点,且直线OA与l的距离等于4,若存在,求l方程;若不存在,请证明。
考题
单选题过点(4,-1,3)且平行于直线L:(x-3)/2=y=(z-1)/5的直线方程为().A
(x-4)/2=(y+1)/0=(z-3)/5B
(x-4)/2=(y+1)/1=(z-3)/5C
(x+4)/2=(y-1)/0=(z+3)/5D
(x+4)/2=(y-1)/1=(z+3)/5
热门标签
最新试卷