网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设总体X服从均匀分布U(1,θ),
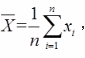
则θ的矩估计为( )。
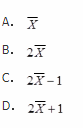
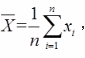
则θ的矩估计为( )。
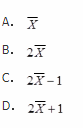
参考答案
参考解析
解析:均匀分布U(a,b)的概率密度为:


更多 “设总体X服从均匀分布U(1,θ), 则θ的矩估计为( )。 ” 相关考题
考题
设x1,x2,x3,…,x25是从均匀分布U(0,5)中抽取的一个样本,则样本均值近似服从的分布为________。A.N(5,1/2)B.N(5,1/10)C.N(2.5,1/12)D.N(2.5,1/10)
考题
设X在[0,1]上服从均匀分布,Y=2X+1,则下列结论正确的是()A、Y在[0,1]上服从均匀分布B、Y在[1,3]上服从均匀分布C、Y在[0,3]上服从均匀分布D、P{0≤Y≤1}=1
考题
问答题总体X在[0,1]上服从均匀分布,x1,x2,…,x8为其样本,,则____.
热门标签
最新试卷