考题
设X1,X2,…,X16是来自总体X~N(4,б2)的简单随机样本,б2已知,令,则统计量服从的概率密度函数为()
考题
设(X1,X2,…,Xn)(N≥2)为标准正态总体X的简单随机样本,则().
考题
设(X1,X2,X3)为来自总体X的简单随机样本,则下列不是统计量的是().
考题
设总体X~N(μ,σ^2),X1,X2,…,Xn为总体X的简单随机样本,X与S^2分别为样本均值与样本方差,则().
考题
设总体X在区间(0,θ)内服从均匀分布,X1,X2,X3是来自总体的简单随机样本.证明:与都是参数θ的无偏估计量,试比较其有效性.
考题
设总体X服从参数为2的指数分布,X1,X2,…,Xn为来自总体X的简单随机样本,则当n→∞时,依概率收敛于_______.
考题
设X1,X2,…,X7是总体X~N(0,4)的简单随机样本,求P
考题
设总体X的分布函数为
其中未知参数β>1,X1,X2,…,Xn为来自总体X的简单随机样本,求:
(Ⅰ)β的矩估计量;(Ⅱ)β的最大似然估计量.
考题
设总体X~N(0,σ^2),X1,X2,…,X20是总体X的简单样本,求统计量U=所服从的分布.
考题
设总体X的分布律为P(X=k)P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.
考题
设总体X~N(μ,25),X1,X2,…,X100为来自总体的简单随机样本,求样本均值与总体均值之差不超过1.5的概率
考题
设总体X服从分布N(0,2^2),而X1,X2,…,X15是来自总体X的简单随机样本,则随机变量服从_______分布,参数为________.
考题
设总体X,Y相互独立且都服从N(μ,σ^2)分布,(X1,X2,…,Xn)与(Y1,Y1,…,yn)分别为来自总体X,Y的简单随机样本,证明:为参数σ^2的无偏估计量,
考题
设总体X的分布律为P(X=i)=(i=1,2,…,θ,X1,X2,…,Xn为来自总体的简单随机样本,则θ的矩估计量为_______(其中θ为正整数).
考题
设总体X的密度函数为f(x)=,X1,X2,…,Xn为来自总体X的简单随机样本,求参数θ的最大似然估计量.
考题
设X1,X2,…,Xn是来自总体X的简单随机样本,已知E(X^k)=ak(k=1,2,3,4).
证明:当n充分大时,随机变量近似服从正态分布,并指出其分布参数.
考题
设总体X的密度函数为f(x)=,(X1,X2,…,Xn)为来自总体X的简单随机样本.(1)求θ的矩估计量θ;(2)求D(θ).
考题
设总体X的概率密度为f(x)=,其中θ>-1是未知参数,X1,
X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和最大似然估计法求参数θ的估计量.
考题
设总体X服从正态分布N(μ,σ^2)(σ>0),从该总体中抽取简单随机样本X1,X2,…,Xn(n≥2),其样本均值,求统计量的数学期望E(Y).
考题
设X1,X2,…,X9是来自正态总体X的简单随机样本,…证明统计量Z服从自由度为2的t分布.
考题
若总体X~N(0,32),X1,X2,…,x9为来自总体样本容量为9的简单随机样本,则服从_______分布,其自由度为_______.
考题
设总体X服从正态分布N(μ,σ^2)(σ>0),X1,X1,…,Xn为来自总体X的简单随机样本,令Y=.,求Y的数学期望与方差
考题
设总体X的分布函数为
其中θ是未知参数且大于零.X1,X2,…,Xn为来自总体X的简单随机样本.
(Ⅰ)求EX与EX^2;
(Ⅱ)求θ的最大似然估计量.
(Ⅲ)是否存在实数a,使得对任何ε>0,都有?
考题
设总体X的概率密度为
其中参数λ(λ>0)未知,X1,X2,…,Xn是来自总体X的简单随机样本.
(Ⅰ)求参数λ的矩估计量;
(Ⅱ)求参数λ的最大似然估计量.
考题
设总体X的概率密度为
其中μ是已知参数,σ>0是未知参数,A是常数.X1,X2,…,Xn是来自总体X的简单随机样本.
(Ⅰ)求A;
(Ⅱ)求σ的最大似然估计量.
考题
设总体X的概率密度为
其中θ为未知参数且大于零.X1,X2,…,Xn为来自总体X的简单随机样本.
(Ⅰ)求θ的矩估计量;
(Ⅱ)求θ的最大似然估计量.
考题
设总体X的概率密度为
其中θ为未知参数,X1,X2,…,Xn,为来自该总体的简单随机样本.
(Ⅰ)求θ的矩估计量;
(Ⅱ)求θ的最大似然估计量.
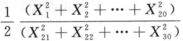 所服从的分布及自由度.
所服从的分布及自由度.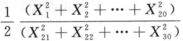 所服从的分布及自由度.
所服从的分布及自由度.
