网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
设二维随机变量(X，Y)在区域上服从均匀分布，令
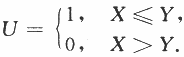
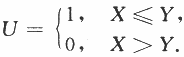
　　(Ⅰ)写出(X，Y)的概率密度；
　　(Ⅱ)请问U与X是否相互独立？并说明理由；
　　(Ⅲ)求Z=U+X的分布函数F(z).

参考答案

参考解析
解析：
更多 “设二维随机变量(X，Y)在区域上服从均匀分布，令 　　(Ⅰ)写出(X，Y)的概率密度； 　　(Ⅱ)请问U与X是否相互独立？并说明理由； 　　(Ⅲ)求Z=U+X的分布函数F(z).” 相关考题
考题 设（X，Y）服从在区域D上的均匀分布，其中D为x轴、y轴及x+y=1所围成，求X与Y的协方差Cov(X,Y).
查看答案
考题 设平面区域D由曲线y=1／x及直线y=0,x=1,x=е2所围成,二维随机变量(X,Y)在区域D上服从均匀分布,则(X,Y)的联合密度函数为()。
查看答案
考题 设随机变量X服从正态分布N（2，4），Y服从均匀分布U（3，5），则E（2X-3Y）= __________.
查看答案
考题 设随机变量X与Y相互独立.已知X服从区间(1，5)上的均匀分布，Y服从参数λ=5的指数分布，则D(3X-5Y)等于( ).A.5 B.9 C.10 D.13
查看答案
考题 设二维随机变量(X，Y)服从二维正态分布，则随机变量ζ=X+Y与η=X-Y不相关的充分必要条件为
查看答案
考题 设X在区间［-2,2］上服从均匀分布,令Y=求： 　　(1)Y,Z的联合分布律；(2)D(Y+Z).
查看答案
考题 设随机变量X在［-1,2］上服从均匀分布,随机变量=则D(Y)=_______.
查看答案
考题 设二维随机变量(X，Y)服从区域G上的均匀分布，其中G是由x-y=0，x+y=2，与y=0所围成的三角形区域. 　　(Ⅰ)求X的概率密度fx(x)； 　　(Ⅱ)求条件概率密度.
查看答案
考题 设X,Y相互独立且都服从(0,2)上的均匀分布,令Z=min{X,Y},则P(0
查看答案
考题 设随机变量X服从参数为2的泊松分布,令Y=4X-3,则E(Y)=_______,D(Y)=_______.
查看答案
考题 设随机变量X服从参数为2的指数分布,证明：Y=1-在区间(0,1)上服从均匀分布.
查看答案
考题 设随机变量(X,Y)在区域D={(z,y)｜0≤x≤2,0≤y≤1}上服从均匀分布,令 　　U=,V=. 　　(1)求(U,V)的联合分布；(2)求.
查看答案
考题 设随机变量X在区间(0，1)内服从均匀分布，在X=x(0　　(Ⅰ)随机变量X和Y的联合概率密度； 　　(Ⅱ)Y的概率密度； 　　(Ⅲ)概率P{X+Y>1}.
查看答案
考题 设随机变量(X，Y)服从二维正态分布，其概率密度为f(x,y)=1/2π
查看答案
考题 已知二维随机变量（X，Y）服从区域[0，1]×[0，1]上的均匀分布，则（ ）。A.P{X＞0.5}=0.25 B.P{Y＞0.5}=0.25 C.P{max（X，Y）＞0.5}=0.25 D.P{min（X，Y）＞0.5}=0.25
查看答案
考题 设随机变量X，Y相互独立，且X～N(μ，σ2)，Y在[a，b]区间上服从均匀分布，则D(X-2Y)=()。
查看答案
考题 设随机变量X与Y相互独立，且X在区间［0，2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E（XY）等于（）。A、1B、3
查看答案
考题 设随机变量X与Y相互独立且都服从区间[0，1]上的均匀分布，则下列随机变量中服从均匀分布的有（）。A、X2B、X+YC、（X，Y）D、X-Y
查看答案
考题 设随机变量X服从[0，2]上的均匀分布，Y=2X+1，则D（Y）=（）。
查看答案
考题 设二维随机变量（X，Y）在区域D上服从均匀分布，其中D://0≤x≤2，0≤y≤2。记（X，Y）的概率密度为f（x，y），则f（1，1）=（）
查看答案
考题 设（X，Y）在由直线y=x，y=2-x，y=0所围的区域内服从均匀分布，则P{0.1
查看答案
考题 设随机变量X，Y都服从区间[0，1]上的均匀分布，则E（X+Y）=（）A、1/6B、1/2C、1D、2
查看答案
考题 设随机变量X，Y相互独立，且均服从[0，1]上的均匀分布，则服从均匀分布的是（）。A、XYB、（X，Y）C、X—YD、X+Y
查看答案
考题 设随机变量X与Y相互独立，已知X服从区间（1，5）上的均匀分布，Y服从参数λ=5的指数分布，则D（3X-5Y）等于（）．A、5B、9C、10D、13
查看答案
考题 设X在[0，1]上服从均匀分布，Y=2X+1，则下列结论正确的是（）A、Y在[0，1]上服从均匀分布B、Y在[1，3]上服从均匀分布C、Y在[0，3]上服从均匀分布D、P{0≤Y≤1}=1
查看答案
考题 设随机变量X，Y相互独立，其中X在[0，6]上服从均匀分布，Y服从参数为λ=3的泊松分布，记Z=X-2Y，则D（Z）=（）。
查看答案
考题 单选题设随机变量X与Y相互独立，且X在区间［0，2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E（XY）等于（）。A 1B 3
查看答案
热门标签
最新试卷