网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设总体X~N(μ,σ^2),X1,X2,…,Xn为总体X的简单随机样本,X与S^2分别为样本均值与样本方差,则().

参考答案
参考解析
解析: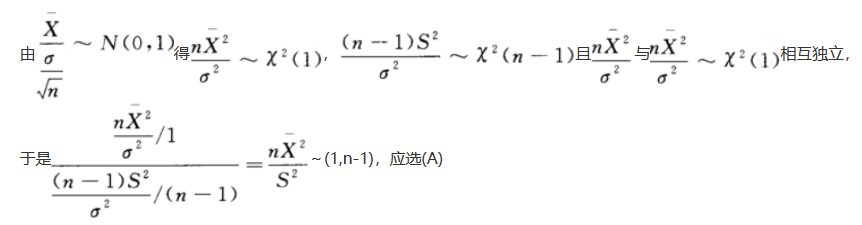
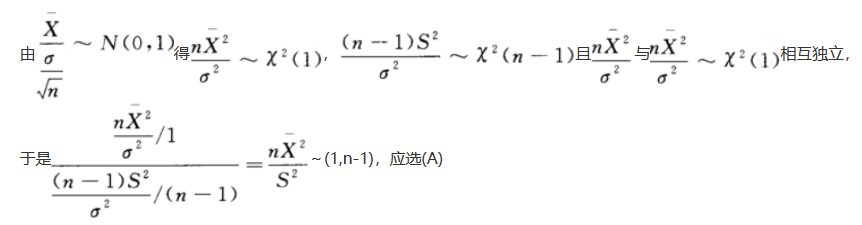
更多 “设总体X~N(μ,σ^2),X1,X2,…,Xn为总体X的简单随机样本,X与S^2分别为样本均值与样本方差,则().” 相关考题
考题
设总体X~B(m,θ),X1,X2,…,Xn为来自该总体的简单随机样本,X为样本均值,则=A.(m-1)nθ(1-θ).
B.m(n-1)θ(1-θ).
C.(m-1)(n-1)θ(1-θ).
D.mnθ(1-θ).
考题
设X1,X2,…Xn是简单随机样本,则有( )。
A. X1,X2,…Xn相互独立 B. X1,X2,…Xn有相同分布
C. X1,X2,…Xn彼此相等 D.X1与(X1,+X2)/2同分布
E.X1与Xn的均值相等
考题
问答题设总体X~N(μ,σ2),x1,x2,…xn为其样本,为样本均值,则____.
热门标签
最新试卷