网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
已知如图，直角三角形ABC的两直角边AC = 8厘米，BC=6厘米，以AC、BC为边向三角形外分别作正方形ACDE和BCFG，再以AB为边向上作正方形ABMN，其中N点落在DE上，BM交CF于点了，则阴影部分的总面积等于（ ）。
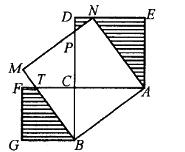
A. 46平方厘米 B. 38平方厘米
C. 40平方厘米 D. 48平方厘米
A. 46平方厘米 B. 38平方厘米
C. 40平方厘米 D. 48平方厘米
参考答案
参考解析
解析：已知ΔABC为直角三角形，AC=8厘米，BC=6厘米，则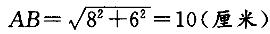
。 设四边形ACPN的面积为S1，ΔBCT的面积为S2，四边形CTMP的面积为S3。SACDE + SBGFC = 82 + 62 =102 =SABMN，即S1 + S2 + S阴影=S1 + S2+ S3 + SΔABC ，故S阴影=S3 + SΔABC 。已知四边形ABMN为正方形，则∠BAC + ∠ABC = ∠ABC + ∠CBM，得∠BAC =∠CBM；∠CBM +∠BPM = ∠CBM +∠BTC，则∠BPM =∠BTC。因为AB=BM，所以SΔABT≌SΔBMP（角角边），故S3+SΔBCT=SΔABC +SΔBCT，得S3=SΔABC。故S阴影=2 SΔABC = 2X8X6/2 = 48(平方厘米)。
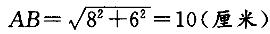。 设四边形ACPN的面积为S1，ΔBCT的面积为S2，四边形CTMP的面积为S3。SACDE + SBGFC = 82 + 62 =102 =SABMN，即S1 + S2 + S阴影=S1 + S2+ S3 + SΔABC ，故S阴影=S3 + SΔABC 。已知四边形ABMN为正方形，则∠BAC + ∠ABC = ∠ABC + ∠CBM，得∠BAC =∠CBM；∠CBM +∠BPM = ∠CBM +∠BTC，则∠BPM =∠BTC。因为AB=BM，所以SΔABT≌SΔBMP（角角边），故S3+SΔBCT=SΔABC +SΔBCT，得S3=SΔABC。故S阴影=2 SΔABC = 2X8X6/2 = 48(平方厘米)。
更多 “已知如图，直角三角形ABC的两直角边AC = 8厘米，BC=6厘米，以AC、BC为边向三角形外分别作正方形ACDE和BCFG，再以AB为边向上作正方形ABMN，其中N点落在DE上，BM交CF于点了，则阴影部分的总面积等于（ ）。 A. 46平方厘米 B. 38平方厘米 C. 40平方厘米 D. 48平方厘米” 相关考题
考题
请教:2009年黑龙江省哈尔滨市中考《数学》试卷第2大题第9小题如何解答?
【题目描述】
18．若正方形ABCD的边长为4，E为BC边上一点，BE＝3，M为线段AE上一点，射线BM交正方形的一边于点F，且BF＝AE，则BM的长为______________．
考题
对边相等,对角相等的凸四边形,是平行四边形吧?
方法①∠B小于90°；左上为A，左下为B，右下为C，右上为D；已知∠B=∠D；AB=CD;证明：过A作AN⊥BC于N；过C作CM⊥AD于M；连接AC∵AN⊥BC；CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D；AB=CD∴△ANB=△DMC(AAS）∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°，AC=AC∴△ACD=△AMD（HL）∴AM=DN又∵BN=DM∴BD=AC∵BD=AC；AB=CD∴凸四边形ABCD为平行四边型。方法②∠B大于90°左上为A，左下为B，右下为C，右上为D；已知∠B=∠D；AB=CD;证明：延长CD,过A作AN⊥BC于N；延长AB,过C作CM⊥AD于M；连接AC∵AN⊥BC；CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D；AB=CD∴△ANB=△DMC(AAS）∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°，AC=AC∴△ACD=△AMD（HL）∴AM=DN又∵BN=DM∴BD=AC∵BD=AC；AB=CD∴凸四边形ABCD为平行四边型。方法③∠B等于90°证明：∵∠B=∠D=90°；AB=CD；AC=AC∴△ABC=△ADC（HL）∴AB=CB∵BD=AC；AB=CD∴凸四边形ABCD为平行四边型。有错吗？若我的证明有错请明示，我知道有个反例，但它是凹四边形。
考题
如图，在以为直径的半圆上取一点C，分别以AC和BC为直径在△ABC外作半圆AEC和BFC。当C点在什么位置时，图中两个弯月形（阴影部分）AEC和BFC的面积和最大？（）
A. AC 大于 BC
B. AC 小于 BC
C. AC 等于 BC
D.无法得出
考题
如图1—15所示，两根轻质细杆AC、BC用铰链固定在墙上构成一个直角三角形支架，在C处挂一盏吊灯。已知AC＝1．2 m，BC＝2 m，吊灯重200 N。求杆AC和BC所受力的大小和方向。
考题
如图，在以AB为直径的半圆上取一点C，分别以AC和BC为直径在AABC外作半圆A￡C和BFC。当C点在什么位置时，图中两个弯月形（阴影部分）AEC和BFC的面积和最大？（ ）
A. AC大于BC
B. AC小于BC
C. AC等于BC
D.无法得出
考题
在边长为1的正方形ABCD中，AC与BD相交于O，以A、B、C、D分别为圆心，以对角线长的一半为半径画圆弧与正方形的边相交，如图，则图中阴影部分的面积为多少?(π=3．14)
A.0．43
B.0．57
C.0．64
D.0．71
考题
如图，一个三棱镜的截面为等腰直角△ABC，∠A为直角，此截面所在平面内的光线沿平行于BC边的方向射到AB边，进入棱镜后直接射到AC边上，并刚好能发生全反射。该棱镜材料的折射率为（ ）。
考题
如图1，在△ABC中，BC = 8 cm，AB的垂直平分线交AB于点Ｄ， 交边AC于点E，△BCE的周长等于18 cm，则AC的长等于（ ）A、6cm
B、8cm
C、10cm
D、12cm
考题
判断题分别在直角三角形三边向外作正五边形，则两直角边上的正五边形的面积之和等于斜边上的正五边形的面积。A
对B
错
热门标签
最新试卷