网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
已知f(χ)是偶函数,且其图像与χ轴有4个交点,则方程f(χ)=0的所有实根之和为( )
A.4
B.2
C.1
D.0
B.2
C.1
D.0
参考答案
参考解析
解析:【考情点拨】本题主要考查的知识点为偶函敷的性质. 【应试指导】设f(χ)=0的实根为
∵f(χ)为偶函数,
∴χ1,χ2,χ3,χ4,两两成对出现(如图),
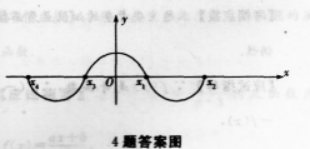


∵f(χ)为偶函数,
∴χ1,χ2,χ3,χ4,两两成对出现(如图),


更多 “已知f(χ)是偶函数,且其图像与χ轴有4个交点,则方程f(χ)=0的所有实根之和为( )A.4 B.2 C.1 D.0” 相关考题
考题
若a,6是方程f(x)=0的两个相异的实根,f(x)在[a,b]上连续,且在(a,b)内可导,则方程f(x)=0在(a,b)内( ).A.只有一个根
B.至少有一个根
C.没有根
D.以上结论都不对
考题
已知二次函数f(x)的二次项系数为实数a,且其图像与直线2x+y=0交点横坐标为1和3.
(1)若方程f(x)+6a=0有两个相等的实数根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数n的取值范围.
考题
已知曲线,其中函数f(t)具有连续导数,且f(0)=0,f'(t)>0(0).若曲线L的切线与x轴的交点到切点的距离恒为1,求函数f(t)的表达式,并求以曲线L及x轴和y轴为边界的区域的面积.
考题
设χ=α是代数方程f(χ)=0的根,则下列结论不正确的是( )。
A、χ-α是f(χ)的因式
B、χ-α整除f(χ)
C、(α,0)是函数y=f(χ)的图象与χ轴的交点
D、f′(α)=O
考题
设x=a是代数方程f(x)=0的根,则下列结论不正确的是( )。
A、 叫是f(x)的因式
B、X-a整除f(x)
C、(a,0)是函数y=f(x)的图象与2轴的交点
D、 f(a)=0
考题
用简单迭代法求方程f(x)=0的实根,把方程f(x)=0表示成x=φ(x),则f(x)=0的根是()。A、y=φ(x)与x轴交点的横坐标B、y=x与y=φ(x)交点的横坐标C、y=x与x轴的交点的横坐标D、y=x与y=φ(x)的交点
考题
若a,b是方程f(x)=0的两个相异的实根,f(x)在[a,b]上连续,且在(a,b)内可导,则方程f’(x)=0在(a,b)内().A、只有一个根B、至少有一个根C、没有根D、以上结论都不对
考题
单选题若f(x)在区间[a,+∞)上二阶可导,且f(a)=A>0,f′(a)<0,f″(x)<0(x>a),则方程f(x)=0在(a,+∞)内( )。A
没有实根B
有两个实根C
有无穷多个实根D
有且仅有一个实根
考题
单选题设f(x)=x(x-1)(x-2),则方程f'(x)=0的实根个数是:A
3B
2C
1D
0
热门标签
最新试卷