网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设A,B为n阶矩阵,考虑以下命题:①若A,B为等价矩阵,则A,B的行向量组等价②若行列式. ,则A,B为等价矩阵③若
,则A,B为等价矩阵③若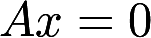 与
与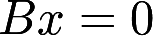 都只有零解,则A,B为等价矩阵④若A,B为相似矩阵,则
都只有零解,则A,B为等价矩阵④若A,B为相似矩阵,则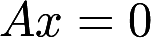 与
与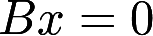 的解空间的维数相同以上命题中正确的是( ).
的解空间的维数相同以上命题中正确的是( ).
 ,则A,B为等价矩阵③若
,则A,B为等价矩阵③若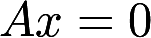 与
与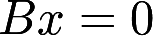 都只有零解,则A,B为等价矩阵④若A,B为相似矩阵,则
都只有零解,则A,B为等价矩阵④若A,B为相似矩阵,则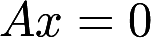 与
与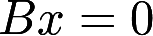 的解空间的维数相同以上命题中正确的是( ).
的解空间的维数相同以上命题中正确的是( ).
A.①③
B.②④
C.②③
D.③④
B.②④
C.②③
D.③④
参考答案
参考解析
解析:

更多 “设A,B为n阶矩阵,考虑以下命题:①若A,B为等价矩阵,则A,B的行向量组等价②若行列式.,则A,B为等价矩阵③若与都只有零解,则A,B为等价矩阵④若A,B为相似矩阵,则与的解空间的维数相同以上命题中正确的是( ). A.①③ B.②④ C.②③ D.③④” 相关考题
考题
设A为m*n矩阵,则有()。
A、若mn,则有ax=b无穷多解B、若mn,则有ax=0非零解,且基础解系含有n-m个线性无关解向量;C、若A有n阶子式不为零,则Ax=b有唯一解;D、若A有n阶子式不为零,则Ax=0仅有零解。
考题
设有方程组AX=O与BX=0,其中A,B都是m×N阶矩阵,下列四个命题:
(1)若AX=O的解都是BX=O的解,则r(A)≥r(B)
(2)若r(A)≥r(B),则AX=0的解都是BX=0的解
(3)若AX=0与BX=0同解,则r(A)-r(B)
(4)若r(A)=r(B),则AX=0与BX=0同解
以上命题正确的是().A.(1)(2)
B.(1)(3)
C.(2)(4)
D.(3)(4)
考题
设A是m×n阶矩阵,则下列命题正确的是().A.若mB.若m>n,则方程组AX=b一定有唯一解
C.若r(A)=n,则方程组AX=b一定有唯一解
D.若r(A)=m,则方程组AX=b一定有解
考题
设A,B为n阶矩阵,考虑以下命题:①若A,B为等价矩阵,则A,B的行向量组等价②若行列式.,则A,B为等价矩阵③若与都只有零解,则A,B为等价矩阵④若A,B为相似矩阵,则与的解空间的维数相同以上命题中正确的是( ).
A.①③
B.②④
C.②③
D.③④
考题
设A是m×n阶矩阵,下列命题正确的是().A.若方程组AX=0只有零解,则方程组AX=b有唯一解
B.若方程组AX=0有非零解,则方程组AX=b有无穷多个解
C.若方程组AX=b无解,则方程组AX=0一定有非零解
D.若方程组AX=b有无穷多个解,则方程组AX=0一定有非零解
考题
设有齐次线性方程组Ax=0和Bx=0,其中A,B均m×n矩阵,现有4个命题:
①若Ax=0的解均是Bx=0的解,则秩(A)≥秩(B);
②若秩(A)≥秩(B),则Ax=0的解均是Bx=0的解;
③若Ax=0与Bx=0同解,则秩(A)=秩(B);
④若秩(A)=秩(B)则Ax=0与Bx=0同解;
以上命题中正确的是A.①②.
B.①③.
C.②④.
D.③④,
考题
设矩阵A,B,C均为n阶矩阵,若AB=C,且B可逆,则( )
A.矩阵C的行向量组与矩阵A的行向量组等价
B.矩阵C的列向量组与矩阵A的列向量组等价
C.矩阵C的行向量组与矩阵B的行向量组等价
D.矩阵C的行向量组与矩阵B的列向量组等价
考题
下列结论中正确的是( )。
A、 矩阵A的行秩与列秩可以不等
B、 秩为r的矩阵中,所有r阶子式均不为零
C、 若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零
D、 秩为r的矩阵中,不存在等于零的r-1阶子式
考题
设A,B,C均为n阶矩阵,若AB=C,且B可逆,则
A.A矩阵C的行向量组与矩阵A的行向量组等价
B.矩阵C的列向量组与矩阵A的列向量组等价
C.矩阵C的行向量组与矩阵B的行向量组等价
D.矩阵C的列向量组与矩阵B的列向量组等价
考题
设有齐次线性方程组Ax=0及Bx=0,其中A、B均为m×n矩阵,现有以下4个命题 ①若Ax=0的解均是Bx=0的解,则rA≥rB; ②若rA≥rB,则Ax=0的解均是Bx=0的解; ③若Ax=0与Bx=0同解,则rA=rB; ④若rA=rB,则Ax=0与Bx=0同解。 以上命题中正确的是()。A、①②B、①③C、②④D、③④
考题
单选题设A为m×n矩阵,B为n×m矩阵,E为m阶单位矩阵,若AB=E,则( )。A
r(A)=m,r(B)=mB
r(A)=m,r(B)=nC
r(A)=n,r(B)=mD
r(A)=n,r(B)=n
考题
单选题设有齐次线性方程组Ax=0及Bx=0,其中A、B均为m×n矩阵,现有以下4个命题 ①若Ax=0的解均是Bx=0的解,则rA≥rB; ②若rA≥rB,则Ax=0的解均是Bx=0的解; ③若Ax=0与Bx=0同解,则rA=rB; ④若rA=rB,则Ax=0与Bx=0同解。 以上命题中正确的是()。A
①②B
①③C
②④D
③④
考题
单选题若A为m×n矩阵,B为n×m矩阵,则( )。A
当m>n时,ABX(→)=0(→)必有非零解B
当m>n时,AB必可逆C
当n>m时,ABX(→)=0(→)只有零解D
当n>m时,必有r(AB)<m
考题
单选题下列结论中正确的是( )A
矩阵A的行秩与列秩可以不等B
秩为r的矩阵中,所有r阶子式均不为零C
若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零D
秩为r的矩阵中,不存在等于零的r-1阶子式
热门标签
最新试卷