网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
设随机变量X～N(0，1)，Y～N(1，4)，且相关系数ρXY=1，则
A.AP{Y=-2X-1}=1
B.P{Y=2X-1}=1
C.P{Y=-2X+1}=1
D.P{Y=2X+1}=1
B.P{Y=2X-1}=1
C.P{Y=-2X+1}=1
D.P{Y=2X+1}=1
参考答案
参考解析
解析：由相关系数的性质可知：如果|ρXY|=1，则必有P{Y=aX+b}=1，(a≠0)，现在题设条件ρXY=1，只要在P{Y=±2X±1}=1四个选项中选一就可以了，实际上只要确定它们的正负号即可，本题可以从X～N(0，1)和Y～N(1，4)及ρXY=1直接推出P{Y=aX+b}=1中的a，b值.但更方便的，不如直接定出a，b的正负号更简单.
【求解】先来确定常数b，由P{Y=aX+b}=1.可得到E(Y)=aE(X)+b再因为X～N(0，1)，Y～N(1，4)，所以，1=a?0+b，即得b=1现来求常数a，实际上只要判定a的正负号就可以了.
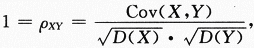
而Cov(X,Y)=Cov(X,aX+b)=aCov(X,X)=a故a>0.答案应选(D).
【评注】从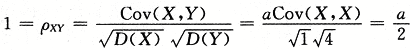
，也可得到a=2
【求解】先来确定常数b，由P{Y=aX+b}=1.可得到E(Y)=aE(X)+b再因为X～N(0，1)，Y～N(1，4)，所以，1=a?0+b，即得b=1现来求常数a，实际上只要判定a的正负号就可以了.
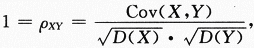
而Cov(X,Y)=Cov(X,aX+b)=aCov(X,X)=a故a>0.答案应选(D).
【评注】从
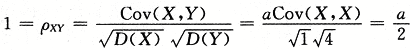，也可得到a=2
更多 “设随机变量X～N(0，1)，Y～N(1，4)，且相关系数ρXY=1，则 A.AP{Y=-2X-1}=1 B.P{Y=2X-1}=1 C.P{Y=-2X+1}=1 D.P{Y=2X+1}=1 ” 相关考题
考题
设随机变量X～N(1,2),Y～N(-1,2),Z～N(0,9)且随机变量X,Y,Z相互独立,已知a(X+Y)2＋bZ2～χ2(n)(ab≠O),则a=_______,b=_______,Z=_______.
考题
设随机变量X与Y相互独立，且X服从标准正态分布N(0，1)，Y的概率分布为P{Y=0}=P{Y=1}=.记Fz(z)为随机变量Z=XY的分布函数，则函数Fz(z)的间断点个数为 A.A0
B.1
C.2
D.3
考题
单选题设随机变量X～N（0，1），Y～N（1，4），且相关系数ρXY＝1，则（ ）。A
P{Y＝－2X－1}＝1B
P{Y＝2X－1}＝1C
P{Y＝－2X＋1}＝1D
P{Y＝2X＋1}＝1
考题
单选题设随机变量X～N（0，1），Y～N（0，4），且相关系数ρXY=1，则（ ）.A
P{Y=-2X-1}=1B
P{Y=2X-1}=1C
P{Y=-2X+1}=1D
P{Y=2X+1}=1
热门标签
最新试卷