网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
如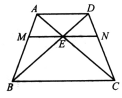
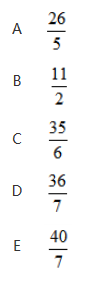
，梯形ABCD的上底与下底分别为5，7，E为AC与BD的交点，MN过点E且平行于AD．则MN=
，梯形ABCD的上底与下底分别为5，7，E为AC与BD的交点，MN过点E且平行于AD．则MN=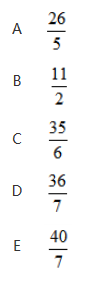参考答案
参考解析
解析：
更多 “如，梯形ABCD的上底与下底分别为5，7，E为AC与BD的交点，MN过点E且平行于AD．则MN=” 相关考题
考题
对边相等,对角相等的凸四边形,是平行四边形吧?
方法①∠B小于90°；左上为A，左下为B，右下为C，右上为D；已知∠B=∠D；AB=CD;证明：过A作AN⊥BC于N；过C作CM⊥AD于M；连接AC∵AN⊥BC；CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D；AB=CD∴△ANB=△DMC(AAS）∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°，AC=AC∴△ACD=△AMD（HL）∴AM=DN又∵BN=DM∴BD=AC∵BD=AC；AB=CD∴凸四边形ABCD为平行四边型。方法②∠B大于90°左上为A，左下为B，右下为C，右上为D；已知∠B=∠D；AB=CD;证明：延长CD,过A作AN⊥BC于N；延长AB,过C作CM⊥AD于M；连接AC∵AN⊥BC；CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D；AB=CD∴△ANB=△DMC(AAS）∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°，AC=AC∴△ACD=△AMD（HL）∴AM=DN又∵BN=DM∴BD=AC∵BD=AC；AB=CD∴凸四边形ABCD为平行四边型。方法③∠B等于90°证明：∵∠B=∠D=90°；AB=CD；AC=AC∴△ABC=△ADC（HL）∴AB=CB∵BD=AC；AB=CD∴凸四边形ABCD为平行四边型。有错吗？若我的证明有错请明示，我知道有个反例，但它是凹四边形。
考题
已知某瞬时平面图形上O点的加速度为a0。图形的角速度ω=0，角加速度为α0。则图形上过O点并垂直于a0的直线mn上各点加速度的方向应是( )。
A.指向O点
B.垂直mn直线
C.与mn直线成θ角
D.沿mn直线背离O点
考题
设抛物线y=1-x2与x轴的交点为A，B，在它们所围成的平面区域内，以线段AB为下底作内接等腰梯形ABCD(如图1—2-2所示)．设梯形上底CD长为2x，面积为S(x)．
图1一2—1
图1—2—2
①写出S(x)的表达式；
②求S(x)的最大值．
考题
如图，在Rt△ACB中，∠ACB=90o,AC=15，BC=20，M是AB边上的动点(与A，B不重合)，N是BC上的动点(与B，C不重合)。
(1)当MN∥AC且BM=12．5时，求线段MN的长。
(2)当MN与AC不平行时，△CMN可能成为直角三角形吗?若可能，请写出线段CN长的取值范围；若不可能，请说明理由。
考题
如右图所示，梯形ABCD的对角线AC⊥BD,其中AD＝1/2,BC＝3,AC＝14/5 ,BD＝2.1.问梯形ABCD的高AE的值是：
A. 43/24
B. 1.72
C. 42/25
D. 1.81
考题
平行四边形ABCD如右图所示，E为AB上的一点，F、G分别是AC和DE、DB的交点。若AB=3AE，则四边形BEFG与ABCD的面积之比是：
A.2︰7
B.3︰13
C.4︰19
D.5︰24
考题
如图，在梯形A.B.C.D.中，,，A.C.交B.D.于O点，过O作A.B.的平行线交B.C.于E点，连结D.E交A.C.于F点，过F作A.B.的平行线交B.C.于G点，连结D.G交A.C.于M点，过M作A.B.的平行线交B.C.于N点，则线段MN的长为：A.2/3
B.5/6
C.7/11
D.6/25
考题
如，等腰梯形的上底与腰均为x，下底为x+10.则x=13.（1）该梯形的上底与下底之比为13：23.（2）该梯形的面积为216.A.条件（1）充分，但条件（2）不充分。
B.条件（2）充分，但条件（1）不充分。
C.条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分。
D.条件（1）充分，条件（2）也充分。
E.条件（1）和（2）单独都不充分，条件（1）和（2）联合起来也不充分。
考题
两根相距为l的平行直导轨ab,cd，bd间连有一固定电阻R，导轨电阻可忽略不计．MN为放在导轨ab和cb上的一长度也为L的导体杆，与ab垂直，其电阻为1/2R，整个装置处于匀强磁场中，磁感应强度的大小为B，方向垂直于导轨所在平面(指向图中纸面内)，现使MN沿导轨方向以速度V向右匀速运动，用U表示MN两端电压，则()。
考题
设抛物线Y=1-x2与x轴的交点为A、B，在抛物线与x轴所围成的平面区域内，以线段AB为下底作内接等腰梯形ABCD(如图2—1所示)．设梯形上底CD长为2x，面积为
S(x)．
(1)写出S(x)的表达式；
(2)求S(x)的最大值．
考题
某店E恰在等高线上，则该点高程既为该等高线的高程。某点A位于两等高线之间（He=29m），这时，可通过A点作大致垂直于相邻两等高线的线段mn，两处mn与mA之图上距离为5/9，则Ha=（）。A、29.44mB、29.56mC、30.44mD、30.56m
考题
填空题已知梯形上、下底长分别为6，8，一腰长为7，则另一腰a的范围是____；若这腰为奇数，则此梯形为____梯形．
热门标签
最新试卷
