网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
如图,A-BCD是棱长为3的正四面体,M是棱AB上的一点,且MB=2MA,G是三角形


参考答案
参考解析
解析:将面ABC和面BCD展开至一个平面,如图所示,连接BG、CG。要使MP+PG最小,则P

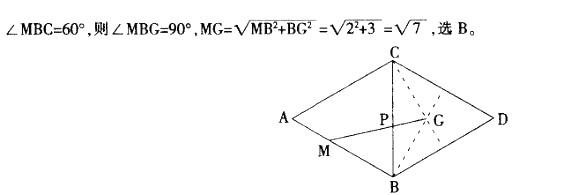


更多 “如图,A-BCD是棱长为3的正四面体,M是棱AB上的一点,且MB=2MA,G是三角形 ” 相关考题
考题
(15)对于四面体ABCD,下列命题正确的是_________(写出所有正确命题的编号)。1相对棱AB与CD所在的直线异面;2由顶点A作四面体的高,其垂足是 BCD的三条高线的交点;3若分别作 ABC和 ABD的边AB上的高,则这两条高所在的直线异面;4分别作三组相对棱中点的连线,所得的三条线段相交于一点;5最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱。
考题
如右图,正四面体P-ABC的棱长为口,D、E、F分别为棱PA、PB、PC的中点,G、H、M分别为DE、EF、FD的中点,则三角形GHM的面积与正四面体P-ABC的表面积之比为:A.1:8B.1:16C.1:32D.1:64
考题
如图,正四面体P-ABC的棱长为a,D、E、F分别为PA、PB、PC的中点,G、H、M 分别为DE,EF,FD的中点,则三角形GHM的面积与正四面体P-ABC的表面积之比为( )。
A. 1 : 8
B. 1 : 16
C. 1 : 32
D. 1 : 64
考题
如图:已知圆0,点P在圆外,D,E在圆上,PE交圆于C,PD与圆相切,G为CE上一点且满足PG=PD,连接DG并延长交圆于A,作弦AB⊥EP,垂足为F。
(1)求证:AB为圆的直径;
(2)若AC=BD,AB=5,求弦DE的长。
考题
如图,正四面体P-ABC的棱长为a,D、E、F分别为棱PA、PB、PC的中点,G、H、M分别为DE、EF、FD的中点,则三角形GHM的面积与正四面体P-ABC的表面积之比为:
A.1:8
B.1:16
C.1:32
D.1:64
考题
连接正四面体侧棱的中点和底面的中心A、E、F、G、H构成多面体
(如右图所示)。问该多面体与正四面体的体积比是多少?( )
A. 1 : 8
B. 1 : 6
C. 1:4
D. 1 : 2
考题
单选题将一个棱长为整数的正方体零件切掉一个角,得到的截面是面积为 100倍根号3的三角形,问其棱长最小为( )A
15B
10C
8D
6
热门标签
最新试卷