如右图，正四面体P-ABC的棱长为口，D、E、F分别为棱PA、PB、PC的中点，G、H、M分别为DE、EF、FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为：A.1：8B.1：16C.1：32D.1：64

题目内容（请给出正确答案）

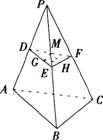
如右图，正四面体P-ABC的棱长为口，D、E、F分别为棱PA、PB、PC的中点，G、H、M分别为DE、EF、FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为：

A.1：8

B.1：16

C.1：32

D.1：64

参考答案

考题在平面上，若两个正三角形的边长的比为1：2，则它们的面积比为1：4，类似地，在空间，若两个正四面体的棱长的比为1：2，则它们的体积比为___________ .

查看答案

考题下列属于不规则单元的有()。 A.正四面体单元B.正三棱体单元C.任意四面体单元D.正六面体单元

查看答案

考题属于不规则单元的有( )。 A、正四面体单元B、正三棱体单元C、任意曲边单元D、任意六面体单元

查看答案

考题不属于规则单元的是( ) 。 A.正四面体单元B.正三棱体单元C.正六面体单元D.曲边单元

查看答案

考题正四面体的棱长增长10％，则表面积增加（）A．21％B．15％C．44％D．40％

查看答案

考题如图，正四面体P-ABC的棱长为a，D、E、F分别为PA、PB、PC的中点，G、H、M 分别为DE，EF，FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为（）。 A. 1 : 8 B. 1 : 16 C. 1 : 32 D. 1 : 64

查看答案

考题如图，正四面体P-ABC的棱长为a，D、E、F分别为棱PA、PB、PC的中点，G、H、M分别为DE、EF、FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为： A.1：8 B.1：16 C.1：32 D.1：64

查看答案

考题如图，A-BCD是棱长为3的正四面体，M是棱AB上的一点，且MB=2MA，G是三角形

查看答案

考题连接正四面体侧棱的中点和底面的中心A、E、F、G、H构成多面体（如右图所示）。问该多面体与正四面体的体积比是多少？（） A. 1 : 8 B. 1 : 6 C. 1：4 D. 1 : 2

查看答案

考题如，正方体ABCD-A′B′C′D′的棱长为2,F是棱C′D′的中点，则AF的长为

查看答案

考题如，六边形ABCDEF是平面与棱长为2的正方体所截得到的，若A，B，D，E分别是相应的棱的中点，则六边形ABCDEF的面积为

查看答案

考题棱长为3的正四面体，以其3个侧面的重心为顶点的三角形面积为：

查看答案

考题如图，已知四棱锥P-ABCD底面ABCD为矩形，侧棱PA⊥ABCD，AB=AP=21/2AD=2，E，F分别为PC，AB的中点。 (I)证明：EF∥面PAD。 (II)求三棱锥B-PFC的体积。

查看答案

考题如图，点P为⊙O上一动点，PA，PB为⊙O的两条弦，BE，AF分别垂直于PA，PB，垂足分别为E，F，若∠P=60°，⊙O的半径为4，则EF的长( )。

查看答案

考题正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为30°。

查看答案

考题单选题相同表面积的四面体、六面体、正十二面体及正二十面体中体积最大的是（　　）A 四面体B 六面体C 正十二面体D 正二十面体

查看答案

考题填空题在四面体P-ABC中共有____对异面直线．

查看答案

热门标签