网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
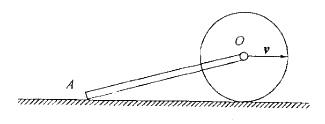
质量为m1的均质杆OA，一端铰接在质量为m2的均质圆盘中心，另一端放在水平面上，圆盘在地面上作纯滚动（如图所示）。圆心速度为v，则系统的动能为：


参考答案

参考解析
解析：提示：平面运动刚体的动能为1/2mvc2+1/2Jcω2。
更多 “质量为m1的均质杆OA，一端铰接在质量为m2的均质圆盘中心，另一端放在水平面上，圆盘在地面上作纯滚动（如图所示）。圆心速度为v，则系统的动能为： ” 相关考题
考题 一端铰接在天花板上的均质木杆作左右摆动,木杆的质量为m,长度为l,木杆自由端的速度为v,角速度为ω,则木杆摆动的动量为mlω。() 此题为判断题(对，错)。
查看答案
考题 均质细直杆AB长为l，质量为m，以匀角速度ω绕O轴转动，如图所示，则AB杆的动能为：
查看答案
考题 质量为m1的均质杆OA，一端铰接在质量为m2的均质圆盘中心，另一端放在水平面上，圆盘在地面上作纯滚动（如图所示）。圆心速度为v，则系统的动能为：
查看答案
考题 均质细直杆OA长为l，质量为m，A端固结一质量为m的小球（不计尺寸），如图所示。当OA杆以匀角速度绕O轴转动时，该系统对O轴的动量矩为：
查看答案
考题 T形均质杆OABC以匀角速度ω绕O轴转动，如图所示。已知OA杆的质量为2m，长为2l，BC杆质量为m，长为l，则T形杆在该位置对O轴的动量矩为：
查看答案
考题 忽略质量的细杆OC=l，其端部固结匀质圆盘。杆上点C为圆盘圆心。盘质量为m，半径为r。系统以角速度ω绕轴O转动，如图所示。系统的动能是：
查看答案
考题 半径为R、质量为m的均质圆轮沿斜面做纯滾动如图所示。已知轮心C的速度为v、加速度为a，则该轮的动能为：
查看答案
考题 忽略质量的细杆OC=l,其端部固结匀质圆盘圆心，盘质量为m,半径为r。系统以角速度w绕轴O转动。系统的动能是：
查看答案
考题 如图，半径为R的圆轮以匀角速度作纯滚动，带动AB杆绕B作定轴转动，D是轮与杆的接触点，如图所示。若取轮心C为动点，杆BA为动坐标系，则动点的牵连速度为（　　）。
查看答案
考题 一半径为r的圆盘以匀角速ω在半径为R的圆形曲面上作纯滚动（如图所示）， 则圆盘边缘上图示M点加速度aM的大小为：
查看答案
考题 匀质杆OA质量为m，长为Z，角速度为ω，如图所示。则其动量大小为：
查看答案
考题 半径为R，质量为m的均质圆盘在其自身平面内作平面运动。在图示位置时，若已知图形上A、B两点的速度方向如图示。α=45o，且知B点速度大小为vB，则圆轮的动能为： A. mvB2/16 B. 3mvB2/16 C. mvB2/4 D. 3mvB2/4
查看答案
考题 均质细直杆OA的质量为m，长为l，以匀角速度W绕O轴转动如图所示，此时将OA杆的惯性力系向O点简化。其惯性力主矢和惯性力主矩的数值分别为（　　）。
查看答案
考题 如图所示，曲柄OA长R，以匀角速度ω绕O轴转动，均质圆轮B在水平面上做纯滚动，其质量为m，半径为r。在图示瞬时，OA杆铅直。圆轮B对接触点C的动量矩为（　　）mRrω。 A．0.5 B．1.0 C．1.5 D．2.0
查看答案
考题 如图所示质量为m1的小车以速度v1在水平路面上缓慢行驶，若在小车上将一质量为m2的货物以相对于小车的速度v2水平抛出，不计地面阻力，则此时小车速度v的大小为（　　）。
查看答案
考题 如图所示，两重物M1和M2的质量分别为m1和m2，两重物系在不计重量的软绳上，绳绕过均质定滑轮，滑轮半径r，质量为M，则此滑轮系统的动量为：
查看答案
考题 图示均质圆轮，质量为m，半径为r，在铅垂图面内绕通过圆轮中心O的水平轴以匀角速度ω转动。则系统动量、对中心O的动量矩、动能的大小为：
查看答案
考题 均质杆OA长L，可在铅直平面内绕水平固定轴O转动。开始杆处在如图所示的稳定平衡位置。今欲使此杆转过1/4转而转到水平位置，应给予杆的另一端A点的速度vA的大小为：
查看答案
考题 如图所示质量为m、长为l的均质杆OA绕O轴在铅垂平面内作定轴转动。已知某瞬时杆的角速度为ω，角加速度为α，则杆惯性力系合力的大小为（　　）。
查看答案
考题 均质细直杆OA长为l ，质量为m，A端固结一质置为m的小球（不计尺寸），如图所示。当OA杆以匀角速度w绕O轴转动时，该系统时O轴的动量矩为：
查看答案
考题 忽略质量的细杆OC=l，其端部固结匀质圆盘。杆上点C为圆盘圆心。盘质量为m，半径为r。系统以角速度ω绕轴O转动。系统的动能是：
查看答案
考题 T形均质杆OABC以匀角速度ω绕O轴转动，如图所示。已知OA杆的质量为2m，长为2l，BC杆质量为m，长为l，则T形杆在图示位置时动量的大小为：
查看答案
考题 如图所示，两重物M1和M2的质量分别为m1和m2，两重物系在不计重量的软绳上，绳绕过均质定滑轮，滑轮半径r，质量为M，则此滑轮系统对转轴O之动量矩为：
查看答案
考题 均质细直杆长为l，质量为m，图示瞬时点A处的速度为v，则杆AB的动量大小为：
查看答案
考题 半径为R、质量为m的均质圆轮沿斜面作纯滚动如图4-75所示。已知轮心C的速度为V、加速度为a,则该轮的动能为（ ）。 A. 1/2mv2 B. 3/2mv2 C. 3/4mv2 D. 1/4mv2
查看答案
考题 如图4-72所示，质量为m1的均质杆OA, 一端较接在质量为m2的均质圆盘中心， 另一端放在水平面上，圆盘在地面上作纯滚动。圆心速度为v,则系统的动能为（ ）。
查看答案
考题 如图4-65所示，忽略质量的细杆OC=l,其端部固结均质圆盘。杆上点C为圆盘圆心。盘质量为m。半径为r。系统以角速度ω绕轴O转动。系统的动能是（ ）。
查看答案
热门标签
最新试卷