网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
f(x)=x-arc cotx,其增减性为( )。
A.在(-∞,+∞)内是单调递增
B.在定义域
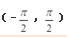
内是单调递增
C.在(-∞,+∞)内是单调递减
D.在定义域
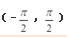
内是单调递减
B.在定义域
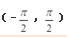
内是单调递增
C.在(-∞,+∞)内是单调递减
D.在定义域
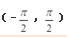
内是单调递减
参考答案
参考解析
解析:arccotx的定义域为(-∞,+∞),从而f(x)的定义域为(-∞,+∞)。可导函数单调性的判定方法为:f′(x)>0时单调上升,f′(x)<0时单调下降;求导得
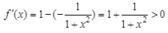
故函数在R上为单调递增函数。
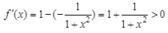
故函数在R上为单调递增函数。
更多 “ f(x)=x-arc cotx,其增减性为( )。 A.在(-∞,+∞)内是单调递增 B.在定义域 内是单调递增 C.在(-∞,+∞)内是单调递减 D.在定义域 内是单调递减” 相关考题
考题
设f(x)为连续函数,F(x)是f(x)的原函数,则( )。(A) 当f(x)是奇函数时,F(x)必为偶函数(B) 当f(x)是偶函数时,F(x)必为奇函数(C) 当f(x)是周期函数时,F(x)必为周期函数(D) 当f(x)是单增函数时,F(x)必为单增函数(E) 当f(x)是单减函数时,F(x)必为单减函数
考题
设f1(x)和f2(x)为二阶常系数线性齐次微分方程y"+py'+q=0的两个特解, 若由f1(x)和f2(x)能构成该方程的通解,下列哪个方程是其充分条件?
A.f1(x) *f'2(x)-f2(x)f'1(x)=0
B.f1(x) * f’2(x)-f2(x) *f'1(x)≠0
C.f1(x)f'2(x)+f2(x)*f'1(x) =0
D.f1(x)f'2(x)+f2(x)*f'1(x) ≠0
考题
设连续型随机变量X的密度函数为f(x),分布函数为F(x).如果随机变量X与-X分布函数相同,则().
A.F(z)=F(-x)
B.F(x)=F(-x)
C.F(X)=F(-x)
D.f(x)=f(-x)
考题
设函数f(x)在x=a的某个邻域内连续,且f(a)为其极大值,则存在δ>0,当x∈(a-δ,a+δ)时,必有( )。A.(x-a)[f(x)-f(a)]≥0
B.(x-a)[f(x)-f(a)]≤0
C.
D.
考题
设随机变量X~N(μ,σ^2),其分布函数为F(x),则对任意常数a,有().A.F(a+μ)+F(a-μ)=1
B.F(μ+a)+F(μ-a)=1
C.F(a)+F(-a)=1
D.F(a-μ)~-F(μ-a)=1
考题
设F1(x)与F2(x)为两个分布函数,其相应的概率密度f1(x)与f2(x)是连续函数,则必为概率密度的是
A.Af1(x)f2(x)
B.2f2(x)F1(x)
C.f1(x)F2(x)
D.f1(x)F2(x)+f2(x)f1(x)
考题
假设随机变量X的分布函数为F(x),密度函数为f(x).若X与-X有相同的分布函数,则下列各式中正确的是( )《》( )A.F(x)=F(-x);
B.F(x)=-F(-x);
C.f(x)=f(-x);
D.f(x)=-f(-x).
考题
命题“若f(x)为奇函数,则f(-x)为奇函数”的否命题( )。A.若f(x)为偶函数,则f(-x)为偶函数
B.若f(x)不是奇函数,则f(-x)不是奇函数
C.若f(-x)为奇函数,则fD.若f(-x)为奇函数,则f(x)不是奇函数
考题
判断下列公式是否为可合一,若可合一,则求出其最一般合一。 (1)P(a,b),P(x,y) (2)P(f(x),b),P(y,z) (3)P(f(x),y),P(y,f(b)) (4)P(f(y),y,x),P(x,f(a),f(b)) (5)P(x,y),P(y,x)
考题
设F1(x)与F2(x)为两个分布函数,其相应的概率密度f1(x)与f2(x)是连续函数,则必为概率密度的是()A、f1(x)f2(x)B、2f2(x)F1(x)C、f1(x)F2(x)D、f1(x)F2(x)+f2(x)F1(x)
考题
设f1(x)和f2(x)为二阶常系数线性齐次微分方程y″+py′+g=0的两个特解,若由f1(x)和f2(x)能构成该方程的通解,下列哪个方程是其充分条件()?A、f1(x)·f′2(x)-f2(x)f′1(x)=0B、f1(x)·f′2(x)-f2(x)·f′1(x)≠0C、f1(x)f′2(x)+f2(x)·f′1(x)=0D、f1(x)f′2(x)+f2(x)f′1(x)≠0
考题
单选题设f1(x)和f2(x)为二阶常系数线性齐次微分方程y″+py′+q=0的两个特解,若由f1(x)和f2(x)能构成该方程的通解,下列哪个方程是其充分条件?()A
f1(x)f′2(x)-f2(x)f′1(x)=0B
f1(x)f′2(x)-f2(x)f′1(x)≠0C
f1(x)f′2(x)+f2(x)f′1(x)=0D
f1(x)f′2(x)+f2(x)f′1(x)≠0
考题
问答题判断下列公式是否为可合一,若可合一,则求出其最一般合一。 (1)P(a,b),P(x,y) (2)P(f(x),b),P(y,z) (3)P(f(x),y),P(y,f(b)) (4)P(f(y),y,x),P(x,f(a),f(b)) (5)P(x,y),P(y,x)
考题
单选题设X~N(2,22),其概率密度函数为f(x),分布函数F(x),则( )。A
P{X≤0}=P{X≥0}=0.5B
f(-x)=1-f(x)C
F(x)=-F(-x)D
P{X≥2}=P{X<2}=0.5
热门标签
最新试卷