网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
试题一(共 20 分)阅读下列说明和图,回答问题 1 至问题 3,将解答填入答题纸的对应栏内。【说明】设有二维整数数组(矩阵)A[1:m,1:n],其每行元素从左至右是递增的,每列元素从上到下是递增的。以下流程图旨在该矩阵中需找与给定整数 X 相等的数。如果找不到则输出“false”;只要找到一个(可能有多个)就输出“True”以及该元素的下标 i 和 j(注意数组元素的下标从 1 开始)。例如,在如下矩阵中查找整数 8,则输出伟:True,4,12 4 6 94 5 9 106 7 10 128 9 11 13流程图中采用的算法如下:从矩阵的右上角元素开始,按照一定的路线逐个取元素与给定整数 X 进行比较(必要时向左走一步或向下走一步取下一个元素),直到找到相等的数或超出矩阵范围(找不到)。【流程图】
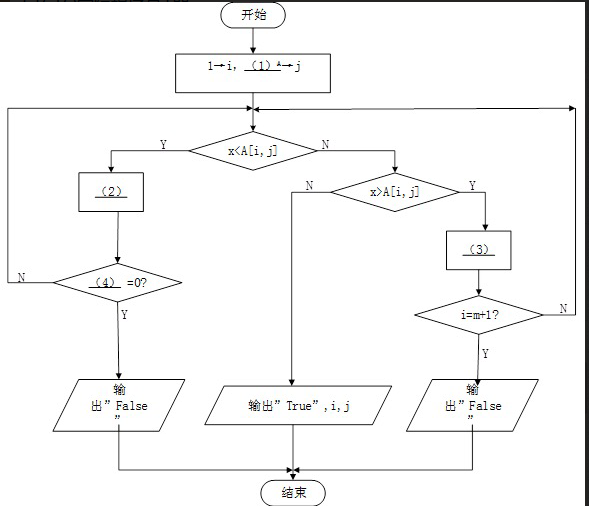
【问题】该算法的时间复杂数是()
供选择答案:A.O(1) B.O(m+n) C.(m*n) D,O(m2+n2)

【问题】该算法的时间复杂数是()
供选择答案:A.O(1) B.O(m+n) C.(m*n) D,O(m2+n2)
参考答案
参考解析
解析:(1)n(2)j-1→j(3)i+1→I(4)j(5)C
【解析】
读题,可以看出元素查找的过程为从右上角开始,往右或者往下进行查找。因此,初始值i=1,j=n。如果查找值小于右上角值,则往右移动一位再进行比较。所以,第二空填j-1→j 。接下来是判断什么时候跳出循环。此时,终止循环的条件是:j=0,也就是其从最右端移到了最左端。再看X
【解析】
读题,可以看出元素查找的过程为从右上角开始,往右或者往下进行查找。因此,初始值i=1,j=n。如果查找值小于右上角值,则往右移动一位再进行比较。所以,第二空填j-1→j 。接下来是判断什么时候跳出循环。此时,终止循环的条件是:j=0,也就是其从最右端移到了最左端。再看X
更多 “试题一(共 20 分)阅读下列说明和图,回答问题 1 至问题 3,将解答填入答题纸的对应栏内。【说明】设有二维整数数组(矩阵)A[1:m,1:n],其每行元素从左至右是递增的,每列元素从上到下是递增的。以下流程图旨在该矩阵中需找与给定整数 X 相等的数。如果找不到则输出“false”;只要找到一个(可能有多个)就输出“True”以及该元素的下标 i 和 j(注意数组元素的下标从 1 开始)。例如,在如下矩阵中查找整数 8,则输出伟:True,4,12 4 6 94 5 9 106 7 10 128 9 11 13流程图中采用的算法如下:从矩阵的右上角元素开始,按照一定的路线逐个取元素与给定整数 X 进行比较(必要时向左走一步或向下走一步取下一个元素),直到找到相等的数或超出矩阵范围(找不到)。【流程图】 【问题】该算法的时间复杂数是() 供选择答案:A.O(1) B.O(m+n) C.(m*n) D,O(m2+n2)” 相关考题
考题
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。【说明】下列流程图用于从数组K中找出一切满足:K(I)+K(J)=M的元素对(K(I),K(J))(1≤I≤J≤N)。假定数组K中的N个不同的整数已按从小到大的顺序排列,M是给定的常数。【流程图】此流程图1中,比较“K(I)+K(J):M”最少执行次数约为(5)。
考题
阅读以下说明和流程图,回答问题将解答填入对应栏。[说明]本流程图实现采用递归函数来求一个整数数组中从元素0到元素n中的最小值。该算法思想是这样的,首先我们假设有一个求数组中最小元素的函数,然后,在求某一具有n的元素的数组的最小值时,只要求将前n-1的元素的最小值与第n个元素比较即可。不断地重复这一过程,直到数组中只剩下一个元素,那么它必定是最小值。注:int min(int X,int y)为返回两数中最小数的函数。int minInArray(int a[],int n)为返回数组中最小数的函数。minA为数组中最小值。[问题l]将流程图的(1)~(4)处补充完整。[问题2]min()函数的定义为(5)。
考题
阅读下列函数说明和C函数,回答问题1~2,将解答填入栏内。[说明]若矩阵Am×n中存在某个元素aij满足:aij…是第i行中最小值且是第j列中的最大值,则称该元素为矩阵A的一个鞍点。下面程序的功能是输出A中所有鞍点,其中参数A使用二维数组表示,m和n分别是矩阵A的行列数。[程序]void saddle (int A[ ] [ ], int m, int n){ int i,j,min;for (i=0;i <m;i + + ){ min: (1);for (j=1; j<n; j+ +)if(A[i][j]<min) (2);for (j=0; j<n; j+ +)if ((3)){ p=0;while (p<m(4))p+ +;if (p > = m)printf ("%d,%d,%d\n",i,j,min);}}}[问题1] 将函数代码中的(1)~(4)处补充完整[问题2]在上述代码的执行过程中,若A为矩阵,则调用saddle(A,3,3)后输出是(5)。
考题
阅读以下说明和流程图,填补流程图中的空缺(1)~(9),将解答填入对应栏内。【说明】假设数组A中的各元素A(1),A(2),…,A(M)已经按从小到大排序(M≥1);数组B中的各元素B(1),B(2),…,B(N)也已经按从小到大排序(N≥1)。执行下面的流程图后,可以将数组A与数组B中所有的元素全都存入数组C中,且按从小到大排序 (注意:序列中相同的数全部保留并不计排列顺序)。例如,设数组A中有元素:2,5, 6,7,9;数组B中有元素2,3,4,7:则数组C中将有元素:2,2,3,4,5,6,7, 7, 9。【流程图】
考题
试题四(共15 分)阅读下列说明和C代码,回答问题 1 至问题3,将解答写在答题纸的对应栏内。【说明】某应用中需要对100000 个整数元素进行排序,每个元素的取值在 0~5 之间。排序算法的基本思想是:对每一个元素 x,确定小于等于 x的元素个数(记为m),将 x放在输出元素序列的第m 个位置。对于元素值重复的情况,依次放入第 m-l、m-2、…个位置。例如,如果元素值小于等于4 的元素个数有 10 个,其中元素值等于 4 的元素个数有3个,则 4 应该在输出元素序列的第10 个位置、第 9 个位置和第8 个位置上。算法具体的步骤为:步骤1:统计每个元素值的个数。步骤2:统计小于等于每个元素值的个数。步骤3:将输入元素序列中的每个元素放入有序的输出元素序列。【C代码】下面是该排序算法的C语言实现。(1)常量和变量说明R:常量,定义元素取值范围中的取值个数,如上述应用中 R值应取6i:循环变量n:待排序元素个数a:输入数组,长度为nb:输出数组,长度为nc:辅助数组,长度为R,其中每个元素表示小于等于下标所对应的元素值的个数。(2)函数sort1 void sort(int n,int a[ ],intb[ ]){2 int c[R],i;3 for (i=0;i (1) ;i++){4 c[i]=0;5 }6 for(i=0;in;i++){7 c[a[i]] = (2) ;8 }9 for(i=1;iR;i++){10 c[i]= (3) ;11 }12 for(i=0;in;i++){13 b[c[a[i]]-1]= (4) ;14 c[a[i]]=c[a[i] ]-1;15 }16 }【问题1】(8 分)根据说明和C代码,填充 C代码中的空缺(1)~(4)。【问题2】(4 分)根据C代码,函数的时间复杂度和空间复杂度分别为 (5) 和 (6) (用 O符号表示)。【问题3】(3 分)根据以上C代码,分析该排序算法是否稳定。若稳定,请简要说明(不超过 100 字);若不稳定,请修改其中代码使其稳定(给出要修改的行号和修改后的代码)。从下列的2 道试题(试题五和试题六)中任选 1 道解答。如果解答的试题数超过 道,则题号小的 道解答有效。
考题
阅读以下说明和流程图将应填入(n)处的字句写在答题纸的对应栏内【说明】在一个矩阵中如果其零元素的个数远远多于其非零元素的个数时称这样的矩阵为稀疏矩阵稀疏矩阵通常采用三元组数组表示每个非零元素用一个三元组来表示即非零元素的行号列号和它的值然后按某种顺序将全部非零元素的三元组存于一个数组中例如对于以下二维数组其中三元数组a的第行元素的值分别存储稀疏矩阵x的行数列数和非零元素的个数下面的流程图描述了稀疏矩阵转换的过程【流程图】
考题
●设下三角矩阵(上三角部分的元素值都为 0)A[0..n,0..n]如下所示,将该三角矩阵的所有非零元素(即行下标不小于列下标的元素)按行优先压缩存储在容量足够大的数组M[ ]中(下标从1 开始),则元素 A[I,j](O≤i≤n,j≤i)存储在数组M 的 (57) 中。
考题
阅读下列说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。 【说明】 设有二维整数数组(矩阵)A[1:m,1:n],其每行元素从左到右是递增的,每列元素从上到下是递增的。以下流程图旨在该矩阵中需找与给定整数X相等的数。如果找不到则输出false;只要找到一个(可能有多个)就输出True以及该元素的下标i和j(注意数组元素的下标从1开始)。 例如,在如下矩阵中查找整数8,则输出伟:True,4,1 2 4 6 9 4 5 9 10 6 7 10 12 8 9 11 13 流程图中采用的算法如下:从矩阵的右上角元素开始,按照一定的路线逐个取元素与给定整数X进行比较(必要时向左走一步或向下走一步取下一个元素),直到找到相等的数或超出矩阵范围(找不到)。【流程图】【问题】该算法的时间复杂数是() 供选择答案:A.O(1) B.O(m+n) C.O(m*n) D,O(m+n)
考题
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。 【说明】 下面流程图的功能是:在给定的一个整数序列中查找最长的连续递增子序列。设序列存放在数组 A[1:n](n2)中,要求寻找最长递增子序列 A[K: K+L-1] (即A[K]A[K+1]A[K+L-1])。流程图中,用 Kj 和Lj 分别表示动态子序列的起始下标和长度,最后输出最长递增子序列的起始下标 K 和长度 L。 例如,对于序列 A={1 ,2,4,4 ,5,6,8,9,4,5,8},将输出K=4, L=5。【流程图】注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1,格式为: 循环控制变量=初值,终值
考题
阅读以下说明和流程图,填补流程图和问题中的空缺(1)~(5),将解答填入答题纸的对应栏内。 【说明】 设整型数组A[1:N]每个元素的值都是1到N之间的正整数。一般来说,其中会有一些元素的值是重复的,也有些数未出现在数组中。下面流程图的功能是查缺查重,即找出A[1:N]中所有缺的或重复的整数,并计算其出现的次数(出现次数为0时表示缺)。流程图中采用的算法思想是将数组A的下标与值看作是整数集[1:N]加上的一个映射,并用数组C[1:N]记录各整数出现的次数,需输出所有缺少的或重复的数及其出现的次数。【流程图】【问题】 如果数组A[1:5]的元素分别为{3,2,5,5,1},则算法流程结束后输出结果为: (5) 。 输出格式为:缺少或重复的元素,次数(0表示缺少)
考题
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。 【说明】 设有整数数组A[1:N](N1),其元素有正有负。下面的流程图在该数组中寻找连续排列的若干个元素,使其和达到最大值,并输出其起始下标K、元素个数L以及最大的和值M。 例如,若数组元素依次为3,-6,2,4,-2,3,-1,则输出K=3,L=4,M=7。该流程图中考察了A[1:N]中所有从下标i到下标j(ji)的各元素之和S,并动态地记录其最大值M。【流程图】注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1,格式为:循环控制变量=初值,终值
考题
试题一(共15分)阅读以下说明和流程图,填补流程图中的空缺(1)~(5),将解答填入答题纸的对应栏内。【说明】两个包含有限个元素的非空集合A、B的相似度定义为IAUBI/IA U Bl,即它们的交集大小(元素个数)与并集大小之比。以下的流程图计算两个非空整数集合(以数组表示)的交集和并集,并计算其相似度。己知整数组A[1:m】和B【1:n】分别存储了集合A和B的元素(每个集合中包含的元素各不相同),其交集存放于数组C[1:s】,并集存放于数组D【1:t】,集合A和B的相似度存放于SIM。例如,假设A={1,2,3,4},B={1,4,5,6},则C={1,4},D={1,2,3,4,5,6},A与B的相似度SIM=1/3。
考题
阅读下列说明和C代码,回答问题l至问题3.将解答写在答题纸的对应栏内。【说明】计算一个整数数组a的最长递增子序列长度的方法描述如下:假设数组a的长度为n,用数组b的元素b[i]记录以a[i](0≤in)为结尾元素的最长递增子序列的长度,则数组a的最长递增子序列的长度为器;其中b[i]满足最优子结构,可递归定义为:【c代码】下面是算法的c语言实现。(1)常量和变量说明a:长度为n的整数数组,待求其最长递增子序列b:长度为n的数组,b[i]记录以a[i](0≤in)为结尾元素的最长递增子序列的长度,其中0≤inlen:最长递增子序列的长度i.j:循环变量temp,临时变量(2)C程序include stdio . hint maxL (int *b. int n) {int i. temp =0;For(i = 0; i n; i++){if (b[i] temp )Temp= b[i];}Return temp;【问题l】(8分)根据说明和C代码,填充C代码中的空(1)~(4)。【问题2】(4分)根据说明和C代码,算法采用了(5)设计策略,时间复杂度为(6)(用O符号表示)。【问题3】(3分)已知数组a={3,10,5,15,6,8},根据说明和C代码,给出数组b的元素值。
考题
●试题二阅读下列说明、流程图和算法,将应填入(n)处的字句写在答题纸的对应栏内。【说明】下面的流程图(如图3所示)用N-S盒图形式描述了数组A中的元素被划分的过程。其划分方法是:以数组中的第一个元素作为基准数,将小于基准数的元素向低下标端移动,而大于基准数的元素向高下标端移动。当划分结束时,基准数定位于A[i],并且数组中下标小于i的元素的值均小于基准数,下标大于i的元素的值均大于基准数。设数组A的下界为low,上界为high,数组中的元素互不相同。例如,对数组(4,2,8,3,6),以4为基准数的划分过程如下:【流程图】图3流程图【算法说明】将上述划分的思想进一步用于被划分出的数组的两部分,就可以对整个数组实现递增排序。设函数int p(int A[],int low,int high)实现了上述流程图的划分过程并返回基准数在数组A中的下标。递归函数void sort(int A[],int L,int H)的功能是实现数组A中元素的递增排序。【算法】void sort (int A[], int 1,int H){if ( LH){k=p(A,L,R);//p()返回基准数在数组A中的下标sort( (4) );//小于基准数的元素排序sort( (5) );//大于基准数的元素排序}}
考题
●试题一阅读下列说明和流程图,将应填入(n)处的语句写在答题纸的对应栏内。【说明】下列流程图用于从数组K中找出一切满足:K(I)+K(J)=M的元素对(K(I),K(J))(1≤I≤J≤N)。假定数组K中的N个不同的整数已按从小到大的顺序排列,M是给定的常数。【流程图】此流程图1中,比较"K(I)+K(J)∶M"最少执行次数约为 (5) 。图1
考题
试题三(共15分)阅读以下说明和C函数,回答问题 l和问题 2,将解答填入答题纸的对应栏内。【说明】对于具有n个元素的整型数组a,需要进行的处理是删除a中所有的值为 0的数组元素,并将a中所有的非 O元素按照原顺序连续地存储在数组空间的前端。下面分别用函数CompactArr_v1 和CompactArr v2来实现上述处理要求,函数的返回值为非零元素的个数。 函数CompactArr_vl(int a[],int n)的处理思路是:先申请一个与数组a的大小相同的动态数组空间,然后顺序扫描数组a的每一个元素,将遇到的非O元素依次复制到动态数组空间中,最后再将动态数组中的元素传回数组a中。函数CompactArr_v2(int a[],int n)的处理思路是:利用下标i(初值为 0)顺序扫描数组a的每一个元素,下标k(初值为0)表示数组 a中连续存储的非0元素的下标。扫描时,每遇到一个数组元素,i就增 1,而遇到非 0元素并将其前移后k才增 1。【问题1】 (12分)请根据说明中函数CompactArr_v1的处理思路填补空缺(1)~(3),根据CompactArr_v2的处理思路填补空缺(4)。【问题2】(3分)请说明函数CompactArr vl存在的缺点。
考题
试题一(共 15 分)阅读以下说明和流程图,填补流程图中的空缺(1)~(9) ,将解答填入答题纸的对应栏内。[说明]假设数组 A 中的各元素 A(1),A(2) ,…,A(M)已经按从小到大排序(M≥1) ;数组 B 中的各元素 B(1),B(2),…,B(N)也已经按从小到大排序(N≥1) 。执行下面的流程图后, 可以将数组 A 与数组 B 中所有的元素全都存入数组 C 中, 且按从小到大排序 (注意:序列中相同的数全部保留并不计排列顺序) 。例如,设数组 A 中有元素:2,5,6,7,9;数组B 中有元素:2,3,4,7;则数组 C 中将有元素:2,2,3,4,5,6,7,7,9。[流程图]
考题
试题二(共15分)阅读以下说明和C函数,填充函数中的空缺,将解答填入答题纸的对应栏内。【说明】如果矩阵A中的元素A[i,j]满足条件:A[i,j]是第i行中值最小的元素,且又是第j列中值最大的元素,则称之为该矩阵的一个马鞍点。一个矩阵可能存在多个马鞍点,也可能不存在马鞍点。下面的函数求解并输出一个矩阵中的所有马鞍点,最后返回该矩阵中马鞍点的个数。【C函数】Int findSaddle(int a[][N],int M),{ /*a表示M行N列矩阵,N是宏定义符号常量量*/int row,column,i,k;int minElem;int count=0;/*count用于记录矩阵中马鞍点的个数*/for( row = 0;row (1) ;row++) {/*minElem用于表示第row行的最小元素值,其初值设为该行第0列的元素值*/(2) ;for( column = 1;column (3) ;column++)if( minElem a[row][column]) {minElem = a[row][column];}for(k=0;kN;k++)if(a[row][k]==minElem){/术对第row行的每个最小元素,判断其是否为所在列的最大元素*/for(i=0;i M;i++)if( (4) minElem) break;if(i=(5) ){printf("(%d,%d):%d\n",row,k,minElem);/*输出马鞍点*/count++;}/*if*/}/*if*/}/*for*/return count,}/*findSaddle*/
考题
阅读下列说明和C代码,回答问题,将解答填入答题纸的对应栏内。
【说明】
计算一个整数数组a的最长递增子序列长度的方法描述如下:
假设数组a的长度为n,用数组b的元素b[i]记录以a[i](0≤i<n)为结尾元素的最长递增子序列的长度为 ;其中b[i]满足最优子结构,可递归定义为:
【C代码】
下面是算法的C语言实现。
(1)常量和变量说明
a:长度为n的整数数组,待求其最长递增子序列
b:长度为n的数组,b[i]记录以a[i](0≤ilen:最长递增子序列的长度
i, j:循环变量
temp:临时变量
(2)C程序
#include int maxL(int*b, int n) {int i, temp=0;for(i=0; itemp) temp=b[i]; } return temp;}int main() { int n,a[100], b[100], i, j, len; scanf("%d", for(i=0;i
【问题1】(8分)
根据说明和C代码,填充C代码中的空(1)~(4)。
【问题2】(4分)
根据说明和C代码,算法采用了 (5) 设计策略,时间复杂度为 (6) (用O符号表示)。
【问题3】(5分)
已知数组a={3,10,5,15,6,8},据说明和C代码,给出数组b的元素值。
考题
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。
[说明]
两个包含有限个元素的非空集合A、B的相似度定义为|A∩B|/|A∪B|,即它们的交集大小(元素个数)与并集大小之比。
以下的流程图计算两个非空整数集合(以数组表示)的交集和并集,并计算其相似度。已知整数组A[1:m]和B[1:n]分别存储了集合A和B的元素(每个集合中包含的元素各不相同),其交集存放于数组C[1:s],并集存放于数组D[1:t],集合A和B的相似度存放于SIM。
例如,假设A={1,2,3,4},B={1,4,5,6},则C={1,4),D={1,2,3,4,5,6},A与B的相似度SIM=1/3。
[流程图]
考题
阅读下列说明和流程图,填补流程图中的空缺(1)~(9),将解答填入答题纸的对应栏内。【说明】假设数组A中的各元素A⑴,A (2),…,A (M)已经按从小到大排序(M>1):数组B中的各元素B(1) , B (2) . B (N)也已经按从小到大排序(N≥1)。执行下面的流程图后,可以将数组A与数组B中所有的元素全都存入数组C中,且按从小到大排序(注意:序列中相同的数全部保留并不计排列顺序)。例如,设数组A中有元素: 2,5,6,7,9;数组B中有元素: 2,3,4,7;则数组C中将有元素: 2,2,3,4,5,6,7,7,9.
考题
阅读以下说明和流程图,填补流程图中的空缺(1)~(9),将解答填入对应栏内。1、【说明】 假设数组A中的各元素A(1),A(2),…,A(M)已经按从小到大排序(M≥1);数组B中的各元素B(1),B(2),…,B(N)也已经按从小到大排序(N≥1)。执行下面的流程图后,可以将数组A与数组B中所有的元素全都存入数组C中,且按从小到大排序 (注意:序列中相同的数全部保留并不计排列顺序)。例如,设数组A中有元素:2,5, 6,7,9;数组B中有元素2,3,4,7:则数组C中将有元素:2,2,3,4,5,6,7, 7, 9。【流程图】
考题
试题(15 分)阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏 内。【说明】设有整数数组 A[1:N](N>1),其元素有正有负。下面的流程图在该数组 中寻找连续排列的若干个元素,使其和达到最大值,并输出其起始下标 K、元素 个数 L 以及最大的和值 M。例如,若数组元素依次为 3,-6,2,4,-2,3,-1,则输出 K=3,L=4,M=7。 该流程图中考察了 A[1:N]中所有从下标 i 到下标 j(j≥i)的各元素之和 S,并动态地记录其最大值 M。【流程图】
注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为 1,格式为:循环控制变量=初值,终值
考题
第四题 阅读以下说明、C函数和问题,回答问题1和问题2将解答填入答题纸的对应栏内。
【说明】
当数组中的元素已经排列有序时,可以采用折半查找(二分查找)法查找一个元素。下面的函数biSearch(int r[],int low,int high,int key)用非递归方式在数组r中进行二分查找,函数biSearch_rec(int r[],int low,int high,int key)采用递归方式在数组r中进行二分查找,函数的返回值都为所找到元素的下标;若找不到,则返回-1。
【C函数1】
int biSearch(int r[],int low,int high,int key)
//r[low..high] 中的元素按非递减顺序排列
//用二分查找法在数组r中查找与key相同的元素
//若找到则返回该元素在数组r的下标,否则返回-1
{
int mid;
while((1)) {
mid = (low+high)/2 ;
if (key ==r[mid])
return mid;
else if (key (2);
else
(3);
}/*while*/
return -1;
}/*biSearch*/
【C 函数 2】
int biSearch_rec(int r[],int low,int high,int key)
//r[low..high]中的元素按非递减顺序排列
//用二分查找法在数组r中查找与key相同的元素
//若找到则返回该元素在数组r的下标,否则返回-1
{
int mid;
if((4)) {
mid = (low+high)/2 ;
if (key ==r[mid])
return mid;
else if (key return biSearch_rec((5),key);
else
return biSearch_rec((6),key);
}/*if*/
return -1;
}/*biSearch_rec*/ 问题:4.1 (12分)
请填充C函数1和C函数2中的空缺,将解答填入答题纸的对应栏内。 问题:4.2 (3分)
若有序数组中有n个元素,采用二分查找法查找一个元素时,最多与( )个数组元素进行比较,即可确定查找结果。
(7)备选答案:
A.[log2(n+1)] B.[n/2] C.n-1 D.n
考题
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。
【说明】
设有整数数组A[1:N](N>1),其元素有正有负。下面的流程图在该数组中寻找连续排列的若干个元素,使其和达到最大值,并输出其起始下标K、元素个数L以及最大的和值M。
例如,若数组元素依次为3,-6,2,4,-2,3,-1,则输出K=3,L=4,M=7。该流程图中考察了A[1:N]中所有从下标i到下标j(j≥i)的各元素之和S,并动态地记录其最大值M。
【流程图】
注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1,格式为:循环控制变量=初值,终值
考题
填空题设有n阶对称矩阵A,用数组s进行压缩存储,当i≥j时,A的数组元素aij相应于数组s的数组元素的下标为()。(数组元素的下标从1开始)
热门标签
最新试卷