网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
如图⊙O和⊙O’相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连接DB并延长交⊙O于点E.证明:
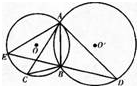
(1)AC?BD=AD?AB;
(2)AC=AE.

(1)AC?BD=AD?AB;
(2)AC=AE.
参考答案
参考解析
解析: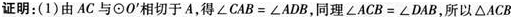

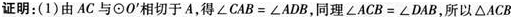


更多 “如图⊙O和⊙O’相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连接DB并延长交⊙O于点E.证明: (1)AC?BD=AD?AB; (2)AC=AE. ” 相关考题
考题
在关系代数运算中,有5种基本运算,它们是( )。A)并(U)、差(.)、交(n)、除(?)和笛卡儿积(?)B)并(u)、差(.)、交(n)、投影(Ⅱ)和选择(o)C)并(U)、交(n)、投影(π)、选择(o)和笛卡儿积(?)D)并(U)、差(-)、投影(Ⅱ)、选择(o)和笛卡儿积(?)
考题
图示两个相啮合的齿轮,A、B分别为齿轮O1,O2上的啮合点,则A、B两点的加速度关系是:
A. aAr=aBr ,aAn=aBn
B. aAr=aBr ,aAn≠aBn
C. aAr≠aBr ,aAn=aBn
D.aAr≠aBr ,aAn≠aBn
考题
图示两个相啮合的齿轮,A、B分别为齿轮O1,O2上的啮合点,则A、B两点的加速度关系是:
A. aAr=aBr ,aAn=aBn B. aAr=aBr ,aAn≠aBn
C. aAr≠aBr ,aAn=aBn D.aAr≠aBr ,aAn≠aBn
考题
如图:已知圆0,点P在圆外,D,E在圆上,PE交圆于C,PD与圆相切,G为CE上一点且满足PG=PD,连接DG并延长交圆于A,作弦AB⊥EP,垂足为F。
(1)求证:AB为圆的直径;
(2)若AC=BD,AB=5,求弦DE的长。
考题
如图,AB是⊙O的直径,AC是弦,直线EF和⊙O相切与点C,AD⊥EF,垂足为D。
(1)若 ∠DAC=63°,求∠BAC;(5分)
(2)若把直线EF向上平行移动,如图,直线EF交 ⊙O于G和C两点,若题中的其他条件不变,这时与∠DAC相等的角是哪一个 为什么 (5分)
考题
如图,在梯形A.B.C.D.中,,,A.C.交B.D.于O点,过O作A.B.的平行线交B.C.于E点,连结D.E交A.C.于F点,过F作A.B.的平行线交B.C.于G点,连结D.G交A.C.于M点,过M作A.B.的平行线交B.C.于N点,则线段MN的长为:A.2/3
B.5/6
C.7/11
D.6/25
考题
如图所示,真空中有A、B两个等量异种点电荷,0、M、N是AB连线的垂线上的三个点,且A O>OB。一个带负电的检验电荷仅在电场力的作用下,从M点运动到N点,其轨迹如图中实线所示。若M、N两点的电势分别为M和N,检验电荷通过M、Ⅳ两点的动能分别为Ekm和Ekn,则( )。
考题
如图所示的是北半球的一段纬线,M、N分别是X日的晨线、昏线与该纬线的交点。X日M、N两点的经度差为90°,一年中M、N两点有重合于O点的现象。读图回答下列小题。
X日后,若M点位置向东接近O点,则太阳直射点()A、位于北半球,且正向北移动B、位于北半球,且正向南移动C、位于南半球,且正向北移动D、位于南半球,且正向南移动
考题
单选题两物标距离定位时,两圆弧位置线交于两点,其中()是观测船位。A
离物标较近的一点B
离物标较近的一点C
靠近推算船位的一点D
离危险物较近的一点
热门标签
最新试卷