网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
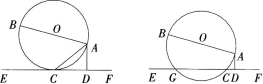
如图,AB是⊙O的直径,AC是弦,直线EF和⊙O相切与点C,AD⊥EF,垂足为D。
(1)若 ∠DAC=63°,求∠BAC;(5分)
(2)若把直线EF向上平行移动,如图,直线EF交 ⊙O于G和C两点,若题中的其他条件不变,这时与∠DAC相等的角是哪一个 为什么 (5分)
(1)若 ∠DAC=63°,求∠BAC;(5分)
(2)若把直线EF向上平行移动,如图,直线EF交 ⊙O于G和C两点,若题中的其他条件不变,这时与∠DAC相等的角是哪一个 为什么 (5分)

参考答案
参考解析
解析:(1)证明:连接OC,则OC⊥EF,且OC=OA,易得∠OCA=∠OAC。 ∵AD⊥EF,∴OC∥AD。∴∠OCA=∠CAD,∴∠CAD=∠OAC=63°
(2)与∠CAD相等的角是∠BAG。
证明如下:如图,连接BG。∵四边形ACGB是⊙O的内接四边形.
∴∠ABG+∠ACG=180°。
∵D,C,G共线,∴∠ACD+∠ACG=180°。
∴∠ACD=∠ABG。
∵AB是⊙O的直径,∴∠BAG+∠ABG=90°
∵AD⊥EF∴∠CAD+∠ACD=90°∴∠CAD=∠BAG
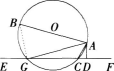
(2)与∠CAD相等的角是∠BAG。
证明如下:如图,连接BG。∵四边形ACGB是⊙O的内接四边形.
∴∠ABG+∠ACG=180°。
∵D,C,G共线,∴∠ACD+∠ACG=180°。
∴∠ACD=∠ABG。
∵AB是⊙O的直径,∴∠BAG+∠ABG=90°
∵AD⊥EF∴∠CAD+∠ACD=90°∴∠CAD=∠BAG

更多 “如图,AB是⊙O的直径,AC是弦,直线EF和⊙O相切与点C,AD⊥EF,垂足为D。 (1)若 ∠DAC=63°,求∠BAC;(5分) (2)若把直线EF向上平行移动,如图,直线EF交 ⊙O于G和C两点,若题中的其他条件不变,这时与∠DAC相等的角是哪一个 为什么 (5分) ” 相关考题
考题
已知a= "ab",那么执行语句b="cd'" & a & " " & "ef"后,变量b的值是()?
A."cd'ab ef"B."cd'abef"C."cdabef"D."cdab ef"
考题
在平行四边形ABCD中,∠DAB=60°,AB=15cm.已知⊙O的半径等于3cm,AB,AD分别与⊙O相切于点E,F,⊙O在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止,试求⊙O滚过的路程.
考题
如果在下图的PC3上运行命令arp122.55.19.3,则得到的MAC地址是( )。A.02-00-54-AD-EF-A1B.02-00-54-AD-EF-B2C.02-00-54-AD-EF-C3D.02-00-54-AD-EF-D4
考题
如图.已知圆⊙O是△ABC的外接圆,AD是圆⊙0的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB。
(1)求证:BE是⊙0的切线;
(2)若BC=√3,AC=5,求圆的直径AD及切线BE的长。
考题
如图:已知圆0,点P在圆外,D,E在圆上,PE交圆于C,PD与圆相切,G为CE上一点且满足PG=PD,连接DG并延长交圆于A,作弦AB⊥EP,垂足为F。
(1)求证:AB为圆的直径;
(2)若AC=BD,AB=5,求弦DE的长。
考题
在平行四边形ABCD中,∠DAB=60,AB=15cm,已知圆O的半径等于3cm,AB,AD分别与圆O相切于点E,F.圆0在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止.试求圆O滚过的路程.
考题
下图为以AC、AD和AF为直径画成的三个圆形,已知AB、BC、CD、DE和EF之间的距离彼此相等。问小圆x、弯月y以及弯月z三部分的面积之比为:
A.4:5:16
B.4:5:14
C.4:7:12
D.4:3:10
考题
如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。
(I)证明:EF∥面PAD。
(II)求三棱锥B-PFC的体积。
考题
如图,在一张矩形纸片ABCD中,AB=4,BC=8。点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点日处,点D落在G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时, 。以上结论中,你认为正确的有( )个。
A.1
B.2
C.3
D.4
考题
直线EF的象限角是南偏西30°,下面的()是正确的。A、REF为S180°WB、REF为S30°WC、直线EF位于第二象限D、直线EF位于第三象限E、αEF为210°
热门标签
最新试卷