网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
已知一批零件的长度X(单位:cm)服从正态分布N(μ,1),从中随机地抽取16个零件,得到长度的平均值为40(cm),则μ的置信度为0.95的置信区间是_______.(注:标准正态分布函数值φ(1.96)=0.975,φ(1.645)=0.95.)
参考答案
参考解析
解析:区间估计不是经常考的一个考点,一般都考单个正态总体方差已知条件下,求期望值μ的置信区间问题,置信区间为: ,其中
,其中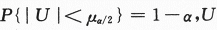 ~N(0,1). 现题给
~N(0,1). 现题给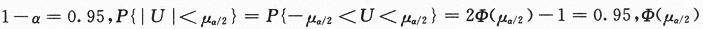 =0.975,查得
=0.975,查得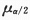 =1.96.将σ=1,n=16,
=1.96.将σ=1,n=16, =40,代入
=40,代入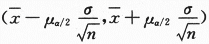 得置信区间
得置信区间
 ,其中
,其中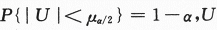 ~N(0,1). 现题给
~N(0,1). 现题给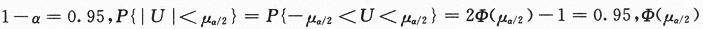 =0.975,查得
=0.975,查得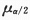 =1.96.将σ=1,n=16,
=1.96.将σ=1,n=16, =40,代入
=40,代入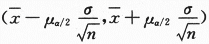 得置信区间
得置信区间
更多 “已知一批零件的长度X(单位:cm)服从正态分布N(μ,1),从中随机地抽取16个零件,得到长度的平均值为40(cm),则μ的置信度为0.95的置信区间是_______.(注:标准正态分布函数值φ(1.96)=0.975,φ(1.645)=0.95.)” 相关考题
考题
假设某总体服从正态分布N(12,4),现从中随机抽取一容量为5的样本X1,X2,X3,X4,X5,则:样本均值与总体均值之差的绝对值大于1的概率是( )。A.0.2628B.0.98C.0.9877D.0.9977
考题
某食品公司生产袋装食品,其容量服从正态分布,规定均值μ=245(ml),标准差σ=3 (ml)。今从中随机抽取32袋,测得样本均值=246(ml)。
当a=0.05时,袋的平均容量是否符合标准规定?()
(u0.95=1. 645,t0.95(31) = 1. 6955,t0.95(32) = 1. 694,t0.975(31) = 2. 04,u0.975=1.96)
A.符合 B.不符合 C.不能确定 D.以上都不对
考题
设X~N(μ,0.09)从中随机抽取样本量为4的样本,其样本均值为,则总体均值μ的0.95的置信区间为()。
A. ±0.15u0.95 B.±0.15u0.975 C. ±0.3u0.95 D.±0.3u0.975
考题
采用包装机包装食盐,要求500g装一袋,已知标准差σ=3g,要使食盐每包平均重量的95%置信区间长度不超过2g,样本量n至少为( )。已知u0.975=1.96, u0.95 = 1. 64。 A. 10 B. 24 C. 35 D. 70
考题
已知某测验结果服从正态分布,总体方差σ2=16,从中随机抽取 100 名被试,其平均值
则总体平均值μ的 95%的置信区间为()A.76.97<μ<78.03
B.77.51<μ<78.49
C.77.2<μ<78.78
D.76.36<μ<78.64
考题
已知随机误差服从N(0,σ2)分布,随机误差落在(-1.96σ,1.96σ)区间内的概率是(),(-3σ,3σ)区间内的概率是()。A、0.95B、0.975C、0.997D、0.90
考题
设某嘴棒长度规范下限为95mm,规范上限为105mm。现检测一批嘴棒长度值,发现检测值服从正态分布N(100,22)(即均值为100,总体标准偏差为2),记Φ(x)为标准正态分布的累积分布函数,则合格品率为()。A、Φ(2.5)-Φ(-2.5)B、Φ(2.5)+Φ(-2.5)C、2Φ(2.5)D、2Φ(2.5)-1
考题
某机械企业在下料时需要把长度为L的钢材截成长度为L1和L2的两段,已知L服从均值为10cm,标准差为0.4cm的正态分布,L1服从均值为5cm,标准差为0.3cm的正态分布,则关于L2的分布,下列说法正确的是()A、一定不是正态分布B、服从均值为5cm,标准差为0.1cm的正态分布C、服从均值为5cm,标准差为0.5cm的正态分布D、服从均值为5cm,标准差为0.7cm的正态分布
考题
已知一批零件的长度X(单位:cm)服从正态分布N(μ,1),从中随机地抽取16个零件,得到长度的平均值为40(cm),则μ的置信度为0.95的置信区间是().A、(37.51,42.49)B、(39.51,40.49)C、(35.51,44.49)D、(36.51,43.49)
考题
单选题已知一批零件的长度X(单位:cm)服从正态分布N(μ,1),从中随机地抽取16个零件,得到长度的平均值为40(cm),则μ的置信度为0.95的置信区间是().A
(37.51,42.49)B
(39.51,40.49)C
(35.51,44.49)D
(36.51,43.49)
考题
单选题某机械企业在下料时需要把长度为L的钢材截成长度为L1和L2的两段,已知L服从均值为10cm,标准差为0.4cm的正态分布,L1服从均值为5cm,标准差为0.3cm的正态分布,则关于L2的分布,下列说法正确的是()A
一定不是正态分布B
服从均值为5cm,标准差为0.1cm的正态分布C
服从均值为5cm,标准差为0.5cm的正态分布D
服从均值为5cm,标准差为0.7cm的正态分布
热门标签
最新试卷