网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设齐次线性方程组
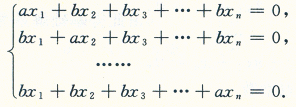
其中a≠0,b≠0,n≥2.试讨论a,b为何值时,方程组仅有零解,有无穷多组解?在有无穷多组解时,求出全部解,并用基础解系表示全部解.
其中a≠0,b≠0,n≥2.试讨论a,b为何值时,方程组仅有零解,有无穷多组解?在有无穷多组解时,求出全部解,并用基础解系表示全部解.
参考答案
参考解析
解析:

更多 “设齐次线性方程组 其中a≠0,b≠0,n≥2.试讨论a,b为何值时,方程组仅有零解,有无穷多组解?在有无穷多组解时,求出全部解,并用基础解系表示全部解.” 相关考题
考题
设A是m×n阶矩阵,Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组,则下列结论正确的是( )。A.若Ax=0仅有零解,则Ax=b有惟一解
B.若Ax=0有非零解,则Ax=b有无穷多个解
C.若Ax=b有无穷多个解,则Ax=0仅有零解
D.若Ax=b有无穷多个解,则Ax=0有非零解
考题
设n阶矩阵A的伴随矩阵A^*≠0,若ζ1,ζ2,ζ3,ζ4是非齐次线性方程组Ax=b的互不相等的解,则对应的齐次线性方程组Ax=0的基础解系A.不存在.
B.仅含一个非零解向量.
C.含有两个线性无关的解向量.
D.含有三个线性无关的解向量.
考题
单选题设A为n阶方阵,则n元齐次线性方程组AX(→)=0(→)仅有零解的充要条件是|A|( )。A
=0B
≠0C
=1D
≠1
热门标签
最新试卷