网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
用配方法化二次型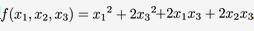 成规范形,并写出所用变换的矩阵.
成规范形,并写出所用变换的矩阵.
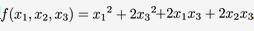 成规范形,并写出所用变换的矩阵.
成规范形,并写出所用变换的矩阵.参考答案
参考解析
解析:

更多 “用配方法化二次型成规范形,并写出所用变换的矩阵.” 相关考题
考题
下列说法正确的是().A.任一个二次型的标准形是唯一的
B.若两个二次型的标准形相同,则两个二次型对应的矩阵的特征值相同
C.若一个二次型的标准形系数中没有负数,则该二次型为正定二次型
D.二次型的标准形不唯一,但规范形是唯一的
考题
设A为可逆的实对称矩阵,则二次型XtAX与XTA^-1X().A.规范形与标准形都不一定相同
B.规范形相同但标准形不一定相同
C.标准形相同但规范形不一定相同
D.规范形和标准形都相同
考题
J27、Y/△-11型的变压器,差动保护的CT二次侧的连接方法是:( )(A)变压器Y、△侧的CT二次侧分别接成△、Y形
(B)变压器Y、△侧的CT二次侧分别接成Y、△形
(C)变压器Y、△侧的CT二次侧均接成△形
(D)变压器Y、△侧的CT二次侧均接成Y形
考题
Y/△-11型的变压器,差动保护的CT二次侧的连接方法是()A、变压器Y、△侧的CT二次侧分别接成△、Y形B、变压器Y、△侧的CT二次侧均接成Y、△形C、变压器Y、△侧的CT二次侧均接成△形D、变压器Y、△侧的CT二次侧均接成T形
热门标签
最新试卷