网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设(X,Y)~f(xy)=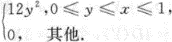
(1)判断X,Y是否独立,说明理由;(2)判断X,Y是否不相关,说明理由;
(3)求Z=X+Y的密度.
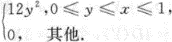
(1)判断X,Y是否独立,说明理由;(2)判断X,Y是否不相关,说明理由;
(3)求Z=X+Y的密度.
参考答案
参考解析
解析: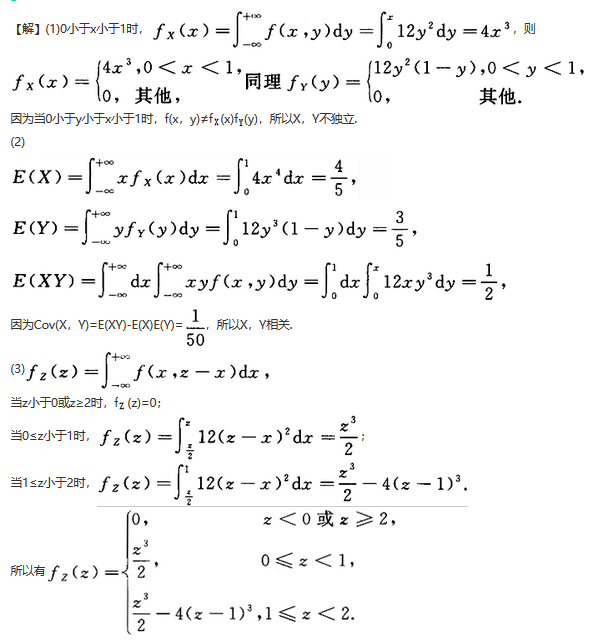
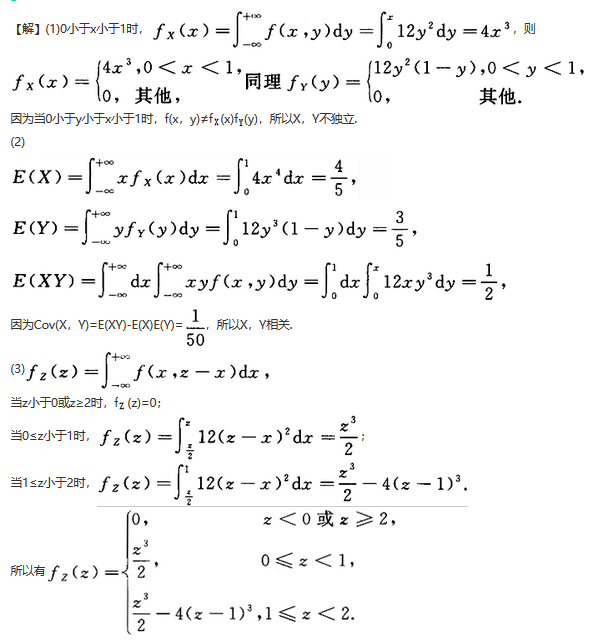
更多 “设(X,Y)~f(xy)= (1)判断X,Y是否独立,说明理由;(2)判断X,Y是否不相关,说明理由; (3)求Z=X+Y的密度.” 相关考题
考题
下列( )项是在D={(x,y)|x2+y2≤1,x≥0,y≥0)上的连续函数f(x,y),且f(x,y)=3(x+y)+16xy。
A.f(x,y)=3(x+y)+32xy
B.f(x,y)=3(x+y)-32xy
C.f(x,y)=3(x+y)-16xy
D.f(x,y)=3(x+y)+16xy
考题
指出下列关系模式是第几范式?并说明理由。 (1)R(X,Y,Z)F={XY→Z} (2)R(x,Y,z)F={Y→z,XZ→Y} (3)R(X,Y,Z)F={Y→Z,Y→X,X→YZ} (4)R(x,Y,z)F={X→Y,X→Z} (5)R(x,Y,Z)F={XY→Z} (6)R(W,X,Y,Z)F={X→Z,WX→Y}
考题
判断下列关系模式可以达到的范式级别: 1)R(X,Y,Z)F={XY→Z} 2)R(X,Y,Z)F={Y→Z,XZ→Y} 3)R(X,Y,Z)F={Y→Z,Y→X,X→YZ} 4)R(X,Y,Z)F={X→Y,X→Z}
考题
F[x]中,有f(x)g(x)=h(x)成立,若将xy代替x可以得到什么?()A、f(xy)g(xy)=h(2xy)B、f(xy)g(xy)=h(xy)C、f(xy)+g(xy)=h(xy)D、[fx+gx]y=hxy
考题
单选题已知函数的全微分df(x,y)=(3x2+4xy-y2+1)dx+(2x2-2xy+3y2-1)dy,则f(x,y)等于( )。A
x3+2x2y-xy2+y3+x-y+CB
x3-2x2y+xy2-y3+x-y+CC
x3+2x2y-xy2+y3-x+y+CD
x3+2xy2-xy2+y3+x-y+C
考题
单选题设z=f(xy,x/y)+g(y/x),其中f、g均可微,则∂z/∂x=( )。A
yf1′+f2′/y-yg′/x2B
yf1′-f2′/y-yg′/x2C
yf1′-f2′/y+yg′/x2D
yf1′+f2′/y+yg′/x2
考题
单选题若函数u=xy·f[(x+y)/xy],f(t)为可微函数,且满足x2∂u/∂x-y2∂u/∂y=G(x,y)u,则G(x,y)必等于( )。A
x+yB
x-yC
x2-y2D
(x+y)2
考题
单选题设函数y=f(x)由方程e2x+y-cos(xy)=e-1所确定,则曲线y=f(x)在点(0,1)处的法线方程为( )。A
y+1=x/2B
y-1=x/2C
y+1=xD
y-1=x
考题
单选题若已知df(x,y)=(x2+2xy-y2)dx+(x2―2xy―y2)dy,则f(x,y)=( )。A
x3/3-x2y+xy2-y3/3B
x3/3-x2y-xy2-y3/3C
x3/3+x2y+xy2-y3/3D
x3/3+x2y-xy2-y3/3+C
考题
单选题F[x]中,有f(x)g(x)=h(x)成立,若将xy代替x可以得到什么?()A
f(xy)g(xy)=h(2xy)B
f(xy)g(xy)=h(xy)C
f(xy)+g(xy)=h(xy)D
[fx+gx]y=hxy
考题
单选题设f(x,y)=ax+by,其中a,b为常数,则f[xy,f(x,y)]=( )。A
xy+bx+b2yB
bxy+ax+byC
bxy+ax-byD
axy+abx+b2y
热门标签
最新试卷