网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设X~N(μ,σ2),σ未知,xi为样本(i=1,2,…,n),H0:μ=μ0,Hi:μ≠μ0,a为显著性水平,则接受域为( )。
A.t<t1-a(n-1)
B.t>ta(n-1)
C.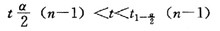
D.以上都不对
参考答案
更多 “ 设X~N(μ,σ2),σ未知,xi为样本(i=1,2,…,n),H0:μ=μ0,Hi:μ≠μ0,a为显著性水平,则接受域为( )。A.t<t1-a(n-1)B.t>ta(n-1)C.D.以上都不对 ” 相关考题
考题
执行下面程序段,语句3的执行次数为______。for(i=0;ii;j++)state;A.n(n+2)/2B
执行下面程序段,语句3的执行次数为______。 for(i=0;i<n-1;i++) for(j=n;j>i;j++) state;A.n(n+2)/2B.(n-1)(n+2)/2C.n(n+1)/2D.(n-1)(n+2)
考题
在正态方差未知时,对正态均值μ的检验问题H0:μ=μ0,H1:μ≠μ0的拒绝域W=( )。A.{|t|>t1-α(n-1)}B.{|t|>tα(n-1)}C.{|t|>t1-α/2(n-1)}D.{|t|>-tα/2(n-1)}E.{|u|>u1-α/2}
考题
一元线性回归模型,Yi=β0+β1X1+μi(i=1,…,n)中,总体方差未知,检验H0:β1=0时,所用的检验统计量服从( )。A.F(1,n-2)B.t(n-1)C.F(1,n-1)D.t(n)
考题
有如下程序段,设n为3的倍数。则语句③的执行频度为______。 Lnt i,j ; ① for(i=i;i<n; i++){ ② if(3*i<=n){ ③ for(j=3*i;j<n;j++){④ x++;y=3*x+2; } } }A.n(n+1)/6B.n(n-1)/6C.n2/6D.(n+1)(n-1)/6
考题
下列程序的时间复杂度为( )。 for (i=l;i<2n;i++) { y++; for(j=0;j<a3n;j++) x++; }A.0(n-1)B.O(2n)C.0(n2)D.O(log2n)
考题
设Xi=(i=1,2,…,16)为正态总体N(0,4)的样本,为样本均值,则的分布可以表示为( )。A.N(0,1/2)B.N(0,4)C.N(0,1/4)D.概率密度为E.N(0,1/8)
考题
设总体X~B(m,θ),X1,X2,…,Xn为来自该总体的简单随机样本,X为样本均值,则=A.(m-1)nθ(1-θ).
B.m(n-1)θ(1-θ).
C.(m-1)(n-1)θ(1-θ).
D.mnθ(1-θ).
考题
在正态方差未知时,对正态均值μ的检验问题H0:μ=μ0 , H1:μ≠μ0 的拒绝域W=( )。
A.{ t >t1-a(n-1)}
B.{ t >ta(n-1)}
C.{ t >t1-a/2(n-1)}
D.{ t >-ta/2(n-1)}
E.{ μ >μ1-a/2}
考题
设Xi=(i= 1, 2, …,16)为正态总体N(0,4)的样本,为样本均值,则的分布可以表示为()。
A. N(0, 1/2) B. N(0, 4)C. N(0, 1/4)
E. N(0, 1/8)
考题
设X1,2X,…,Xn(n>2)相互独立且都服从N(0,1),Yi=Xi-X(i=1,2,…,n).求:
(1)D(Yi)(i=1,2,…,n);(2)Cov(Y1,Yn);(3)P(Yn+Yn≤0).
考题
设(X1,X2,…,X)是抽自正态总体N(0,1)的一个容量为n的样本,记,则下列结论中正确的是()。A、服从正态分布N(0,1)B、n服从正态分布N(0,1)C、服从自由度为n的x2分布D、服从自由度为(n-1)的t分布
考题
单选题设(X1,X2,…,X)是抽自正态总体N(0,1)的一个容量为n的样本,记,则下列结论中正确的是()。A
服从正态分布N(0,1)B
n服从正态分布N(0,1)C
服从自由度为n的x2分布D
服从自由度为(n-1)的t分布
考题
单选题已知X1,X2,…,Xn是从某正态总体随机抽取的一个样本,在μ未知的情况下,对于假设的检验问题H0:σ2=σ20,H1:σ2≠σ20,则给定α下,该检验的拒绝域为( )。A
χ2>χ21-α(n-1)B
χ2<χ2α(n-1)C
χ2>χ21-α/2(n-1)D
χ2<χ21-α/2(n-1)
考题
单选题第0年至第n—1年每年现金流量为A,则其等值于第0年()。A
A·(1+i)n/i(1+i)nB
A·(1+i)n-1/i(1+i)n(1+i)C
A·(1+i)n-1/i(1+i)1+i(1+i)D
A+A·(1+i)n-1/i(1+i)n
热门标签
最新试卷