网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设平面薄板所占Oxy平面上的区域D为1≤x2+y2≤4,x≥0,y≥0,其面密度
u(x,y)=2+y2,求该薄板的质量m.
u(x,y)=2+y2,求该薄板的质量m.
参考答案
参考解析
解析:由二重积分物理意义知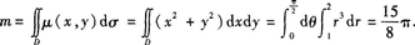
【评析】如果被积函数为f(x2+y2)的形式,积分区域D为圆域或圆的一部分,此时将
 化为极坐标计算常常较简便.
化为极坐标计算常常较简便.
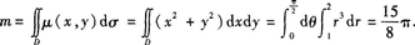
【评析】如果被积函数为f(x2+y2)的形式,积分区域D为圆域或圆的一部分,此时将
 化为极坐标计算常常较简便.
化为极坐标计算常常较简便.
更多 “设平面薄板所占Oxy平面上的区域D为1≤x2+y2≤4,x≥0,y≥0,其面密度 u(x,y)=2+y2,求该薄板的质量m.” 相关考题
考题
设平面π的方程为3x -4y -5z -2 = 0,以下选项中错误的是:
(A)平面π过点(-1,0,-1)
(B)平面π的法向量为-3i + 4 j + 5k
(D) 平面π与平面-2 x -y -2 z + 2 = 0垂直
考题
过点(-1,0,1)且与平面x+y+4z+19=0平行的平面方程为( )。
A. x+y + 4z-3 = 0 B. 2x + y+z-3 = 0
C. x+2y+z-19=0 D. x+2y+4z-9=0
考题
单选题设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=( )。A
1/5B
1/7C
-1/7D
-1/5
考题
单选题设平面α平行于两直线x/2=y/(-2)=z及2x=y=z,且与曲面z=x2+y2+1相切,则α的方程为( )。A
4x+2y-z=0B
4x-2y+z+3=0C
16x+8y-16z+11=0D
16x-8y+8z-1=0
考题
单选题设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=( )。A
1B
-1C
1/7D
-1/7
考题
单选题设平面∏位于平面x-2y+z-2=0和平面x-2y+z-6=0之间,且将二平面间的距离分成1:3,则∏之方程为( )。A
x-2y+z-5=0或x-2y+z-3=0B
x+2y+z+8=0C
x+2y-4z=0D
x-2y+z-8=0
考题
单选题设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=( )。A
-1/2B
-1/4C
-1/7D
-1/9
热门标签
最新试卷