网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
设区域D={(x，y)|-1≤x≤1，-2≤y≤2)，

A.0
B.2
C.4
D.8

参考答案

参考解析
解析：积分区域关于y轴对称，被积函数xy为X的奇函数，可知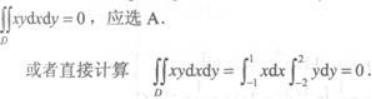
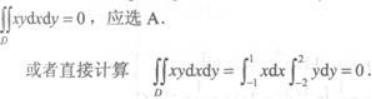
更多 “设区域D={(x，y)|-1≤x≤1，-2≤y≤2)，A.0 B.2 C.4 D.8” 相关考题
考题 设平面区域D由曲线y=1／x及直线y=0,x=1,x=е2所围成,二维随机变量(X,Y)在区域D上服从均匀分布,则(X,Y)的联合密度函数为()。
查看答案
考题 设平面薄板所占xOy平面上的区域D为1≤x2+y2≤4，*≥0，y≥0，其面密度为π(x，y)=x2+y2，求该薄板的质量m。
查看答案
考题 设非齐次线性微分方程y′+P(x)y=Q(x)有两个不同的解y1(x)，y2(x)，C为任意常数，则该方程通解是( )。A.C[y1(x)-y2(x)] B.y1(x)+C[y1(x)-y2(x)] C.C[y1(x)+y2(x)] D.y1(x)+C[y1(x)+y2(x)]
查看答案
考题 设非齐次线性微分方程y+P(x)y=Q(x)有两个不同的解析：y1(x)与y2(x)，C为任意常数，则该方程的通解是( ).A.C[(y1(x)-y2(x)] B.y1(x)+C[(y1(x)-y2(x)] C.C[(y1(x)+y2(x)] D.y1(x)+C[(y1(x)+y2(x)]
查看答案
考题 设D是曲线y=x2与y=1所围闭区域，等于： (A)1 (B) (C)0 (D)2
查看答案
考题 设D是曲线y=x2 与y=1所围闭区域， A. 1 B.1/2 C. 0 D.2
查看答案
考题 设X,Y相互独立,且X～N(1,2),Y～N(0,1),求2=2X－Y＋3的密度函数,
查看答案
考题 设X～P(1),y～P(2),且X,Y相互独立,则P（X+Y=2）=_______.
查看答案
考题 设X,Y为两个随机变量,E(X)=E(Y)=1,D(X)=9,D(Y)=1,且则E（X-2Y+3）……2=_______.
查看答案
考题 设随机变量X～N(0,σ^2),Y～N(0,4σ^2),且P(X≤1,y≤-2)=,则P（X>1,Y>-2）=_______.
查看答案
考题 设随机变量(X,Y)在区域D={(z,y)｜0≤x≤2,0≤y≤1}上服从均匀分布,令 　　U=,V=. 　　(1)求(U,V)的联合分布；(2)求.
查看答案
考题 设(X,Y)在区域D：0　　(1)求随机变量X的边缘密度函数；(2)设Z=2X+1,求D(Z).
查看答案
考题 设随机变量X～N(0，1)，Y～N(1，4)，且相关系数ρXY=1，则 A.AP{Y=-2X-1}=1 B.P{Y=2X-1}=1 C.P{Y=-2X+1}=1 D.P{Y=2X+1}=1
查看答案
考题 设D是曲线y=x2与y=1 所围闭区域，等于( )。 A. 1 B. 1/2 C.0 D. 2
查看答案
考题 设平面薄板所占Oxy平面上的区域D为1≤x2+y2≤4，x≥0，y≥0，其面密度 u(x，y)=2+y2，求该薄板的质量m．
查看答案
考题 设区域D是由直线y=x，x=2，y=1围成的封闭平面图形，
查看答案
考题 设区域D={(x，y)|-1≤x≤1，0≤y≤2}，A.1 B.2 C.3 D.4
查看答案
考题 已知X1=+0010100，Y1=+0100001，X2=0010100，Y2=0100001，试计算下列各式（设字长为8位）。 （1）[X1＋Y1]补=[X1]补＋[Y1]补=（） （2）[X1－Y2]补=[X1]补＋[－Y2]补=（） （3）[X2－Y2]补=[X2]补＋[－Y2]补=（） （4）[X2＋Y2]补=[X2]补＋[Y2]补=（）
查看答案
考题 设二维随机变量（X，Y）在区域D上服从均匀分布，其中D://0≤x≤2，0≤y≤2。记（X，Y）的概率密度为f（x，y），则f（1，1）=（）
查看答案
考题 设X~N（0，1），Y=2X+1，则P{Y-1∣2}=（）
查看答案
考题 填空题设X、Y相互独立，且E（X）＝0，E（Y）＝1，D（X）＝1，D（Y）＝4，则E（X2Y2）＝____。
查看答案
考题 填空题设y1（x）是方程y′＋P（x）y＝f1（x）的一个解，y2（x）是方程y′＋P（x）y＝f2（x）的一个解，则y＝y1（x）＋y2（x）是方程____的解。
查看答案
考题 单选题设y＝y（x）满足∫ydx·∫（1/y）dx＝－1，且当x→＋∞时y→0，y（0）＝1，则y＝（　　）。A ex/2B e－xC exD e－x/2
查看答案
考题 单选题设f（u，v）是二元可微函数，z＝f（y/x，x/y），则x∂z/∂x－y∂z/∂y＝（　　）。A 2（yf1′/x＋xf2′/y）B 2（yf1′/x－xf2′/y）C 2（－yf1′/x＋xf2′/y）D 2（－yf1′/x－xf2′/y）
查看答案
考题 单选题设非齐次线性微分方程y′＋P（x）y＝Q（x）有两个不同的解y1（x），y2（x），C为任意常数，则该方程的通解是（　　）。A C[y1（x）－y2（x）]B y1（x）＋C[y1（x）－y2（x）]C C[y1（x）＋y2（x）]D y1（x）＋C[y1（x）＋y2（x）]
查看答案
考题 单选题设y1（x）是方程y′＋P（x）y＝f1（x）的一个解，y2（x）是方程y′＋P（x）y＝f2（x）的一个解，则y＝y1（x）＋y2（x）是方程（　　）的解。A y′＋P（x）y＝f1（x）＋f2（x）B y＋P（x）y′＝f1（x）－f2（x）C y＋P（x）y′＝f1（x）＋f2（x）D y′＋P（x）y＝f1（x）－f2（x）
查看答案
考题 问答题 设X与Y相互独立,X的概率密度为　　Y的概率密度为　　求：(1)E(2X-3Y+1),D(2X-3Y+1);　　(2)Cov(X,Y)，ρXY.
查看答案
热门标签
最新试卷