网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设f(x)在点x0处可导,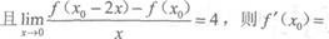 ( )
( )
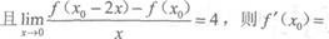 ( )
( )A.4
B.-4
C.2
D.-2
B.-4
C.2
D.-2
参考答案
参考解析
解析: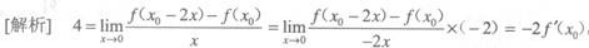
因此f'(x0)=-2,可知选D.
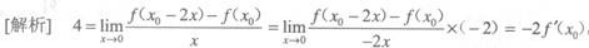
因此f'(x0)=-2,可知选D.
更多 “设f(x)在点x0处可导,( )A.4 B.-4 C.2 D.-2” 相关考题
考题
设f(x)在(-∞,+∞)二阶可导,f'(x0)=0。问f(x)还要满足以下哪个条件,则f(x0)必是f(x)的最大值?
A.x=x0是f(x)的唯一驻点
B.x=x0是f(x)的极大值点
C.f"(x)在(-∞,+∞)恒为负值
D.f"(x0)≠0
考题
设函数f(x)在点x=a处可导,则函数|f(x)|在点x=a处不可导的充分条件是( )A.f(a)=0且f′(a)=0
B.f(a)=0且f′(a)≠0
C.f(a)>0且f′(a)>
D.f(a)<0且f′(a)<
考题
设函数f(x)在定义域I上的导数大于零,若对任意的x0∈I,曲线y=f(x)在点(x0,f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4,且f(0)=2,求f(x)的表达式.
考题
设f(x)在(-∞,+∞)二阶可导,f′(x0)=0。问f(x)还要满足以下哪个条件,则f(x0)必是f(x)的最大值()?A、x=x0是f(x)的唯一驻点B、x=x0是f(x)的极大值点C、f″(x)在(-∞,+∞)恒为负值D、f″(x0)≠0
考题
下列结论不正确的是()。A、z=f(x,y)在点(x0,y0)处可微,则f(x,y)在点(x0,y0)处连续B、z=f(x,y)在点(x0,y0)处可微,则f(x,y)在点(x0,y0)处可导C、z=f(x,y)在点(x0,y0)处可导,则f(x,y)在点(x0,y0)处可微D、z=f(x,y)在点(x0,y0)处偏导数连续,则f(x,y)在点(x0,y0)处连续
考题
设g(x)在(-∞,+∞)严格单调递减,且f(x)在x=x0处有极大值,则必有()。A、g[f(x)]在x=x0处有极大值B、g[f(x)]在x=x0处有极小值C、g[f(x)]在x=x0处有最小值D、g[f(x)]在x=x0既无极值也无最小值
考题
下列结论不正确的是()。A、y=f(x)在点x0处可微,则f(x)在点x0处连续B、y=f(x)在点x0处可微,则f(x)在点x0处可导C、y=f(x)在点x0处连续,则f(x)在点x0处可微D、y=f(x)在点x0处可导,则f(x)在点x0处连续
考题
单选题设f(x)g(x)在x0处可导,且f(x0)=g(x0)=0,f′(x0)g′(x0)>0,f″(x0)、g″(x0)存在,则( )A
x0不是f(x)g(x)的驻点B
x0是f(x)g(x)的驻点,但不是它的极值点C
x0是f(x)g(x)的驻点,且是它的极小值点D
x0是f(x)g(x)的驻点,且是它的极大值点
考题
单选题设f(x)在(-∞,+∞)二阶可导,f(x0)=0。问f(x)还要满足以下哪个条件,则f(x0)必是f(x)的最大值?()A
x=x0是f(x)的唯一驻点B
x=x0是f(x)的极大值点C
f″(x)在(-∞,+∞)恒为负值D
f″(x)≠0
考题
单选题考虑二元函数f(x,y)的下面4条性质:①f(x,y)在点(x0,y0)处连续;②f(x,y)在点(x0,y0)处的两个偏导数连续;③f(x,y)在点(x0,y0)处可微;④f(x,y)在点(x0,y0)处的两个偏导数存在。若用“P⇒Q”表示可由性质P推出Q,则有( )。A
②⇒③⇒①B
③⇒②⇒①C
③⇒④⇒①D
③⇒①⇒④
考题
单选题设y=f(x)满足关系式y″-2y′+4y=0,且f(x0)>0,f′(x0)=0,则f(x)在x0点处( )。A
取得极大值B
取得极小值C
在x0点某邻域内单调增加D
在x0点某邻域内单调减少
考题
单选题下列说法中正确的是( )。[2014年真题]A
若f′(x0)=0,则f(x0)必须是f(x)的极值B
若f(x0)是f(x)的极值,则f(x)在点x0处可导,且f′(x0)=0C
若f(x0)在点x0处可导,则f′(x0)=0是f(x)在x0取得极值的必要条件D
若f(x0)在点x0处可导,则f′(x0)=0是f(x)在x0取得极值的充分条件
考题
单选题设f(x)在(-∞,+∞)二阶可导,f′(x0)=0。问f(x)还要满足以下哪个条件,则f(x0)必是f(x)的最大值()?A
x=x0是f(x)的唯一驻点B
x=x0是f(x)的极大值点C
f″(x)在(-∞,+∞)恒为负值D
f″(x0)≠0
考题
单选题设f(x)在(-∞,+∞)可导,x0≠0,(x0,f(x0))是y=f(x)的拐点,则( )。A
x0必是f′(x)的驻点B
(-x0,-f(x0))必是y=-f(-x)的拐点C
(-x0,-f(x0))必是y=-f(x)的拐点D
对∀x>x0与x<x0,y=f(x)的凸凹性相反
热门标签
最新试卷