网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
将f(x)=e-2X展开为x的幂级数.
参考答案
参考解析
解析: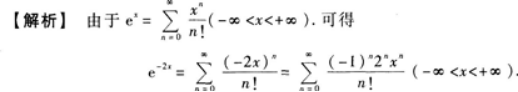 【评析】将函数展开为幂级数,通常将函数与标准展开式中的函数对照.展开为幂级数之后一定要注明收敛域.
【评析】将函数展开为幂级数,通常将函数与标准展开式中的函数对照.展开为幂级数之后一定要注明收敛域.
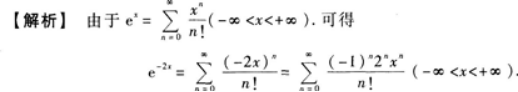 【评析】将函数展开为幂级数,通常将函数与标准展开式中的函数对照.展开为幂级数之后一定要注明收敛域.
【评析】将函数展开为幂级数,通常将函数与标准展开式中的函数对照.展开为幂级数之后一定要注明收敛域.
更多 “将f(x)=e-2X展开为x的幂级数.” 相关考题
考题
单选题y″-4y=e2x的通解为( )。A
y=C1e-2x-(C2+x/4)e-2x(其中C1,C2为任意常数)B
y=C1e-2x+(C2+x/4)e2x(其中C1,C2为任意常数)C
y=C1e-2x+(C2+x/4)e-2x(其中C1,C2为任意常数)D
y=C1e-2x-(C2+x/4)e2x(其中C1,C2为任意常数)
考题
填空题由于高斯投影是按带投影的,在各投影带内()不大,()是一微小量。故可将函数x=x(l,q),y=y(l,q)展开为()的幂级数。
热门标签
最新试卷