网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
已知{an}是由非负整数组成的无穷数列，该数列前n项的最大值记为A。第项之后各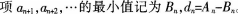
(1)若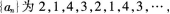
是一个周期为4的数列(即对任意
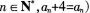写出dl，dz,d3，d0的值；
(2)设d为非负整数，证明：do=一d(n=1，2，3…)的充分必要条件为{an}为公差为d的等差数列：
(3)证明：若a1=2，dn=1(n=1，2，3，…)，则{an}的项只能是1或者2，且有无穷多项为l。
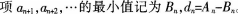
(1)若
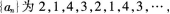是一个周期为4的数列(即对任意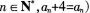写出dl，dz,d3，d0的值；
(2)设d为非负整数，证明：do=一d(n=1，2，3…)的充分必要条件为{an}为公差为d的等差数列：
(3)证明：若a1=2，dn=1(n=1，2，3，…)，则{an}的项只能是1或者2，且有无穷多项为l。
参考答案
参考解析
解析：
更多 “已知{an}是由非负整数组成的无穷数列，该数列前n项的最大值记为A。第项之后各 (1)若是一个周期为4的数列(即对任意写出dl，dz,d3，d0的值； (2)设d为非负整数，证明：do=一d(n=1，2，3…)的充分必要条件为{an}为公差为d的等差数列： (3)证明：若a1=2，dn=1(n=1，2，3，…)，则{an}的项只能是1或者2，且有无穷多项为l。 ” 相关考题
考题
阅读以下说明和流程图，回答问题将解答填入对应栏内。[说明]已知递推数列：a(1)=1，a (2s)= a (s)，a(2s+1)=a (s)+a (s+1)(s 为正整数)。试求该数列的第n项与前n项中哪些项最大?最大值为多少?算法分析：该数列序号分为奇数或偶数两种情况做不同递推，所得数列呈大小有规律的摆动。设置a数组，赋初值a (1)=1。根据递推式，在循环中分项序号s (2～n)为奇数或偶数作不同递推：每得一项 a (s)，即与最大值max 作比较，如果a (s)＞max，则max=a(i)。最后，在所有项中搜索最大项(因最大项可能多于一项)，并打印最大值max。[问题]将流程图中的(1)～(5)处补充完整。注：流程图中(1)循环开始的说明按照“循环变量名：循环初值，循环终值，增量”格式描述。[流程图]
考题
请在函数proc()的横线上填写若干表达式，使从键盘上输入一个整数n，输出斐波那契数列的前n个数。斐波那契数列是一个整数数列，该数列自第3项开始，每个数等于前面两个数之和，即0，1，1，2，3，5，8，13，21，34，55，…注意：部分源程序给出如下。请勿改动main()函数和其他函数中的任何内容，仅在函数proc()的横线上填入所编写的若干表达式或语句。试题程序：
考题
依次取N个(N>1)自然数组成一有穷数列，其中的奇数数列和偶数数列显然都比该自然数数列端短。但是，假如让该自然数数列无限延长，则其中的奇数数列和偶数数列必定不小于整体；在无穷的世界里，部分可能等于整体。下面哪一项不可能是上面结论的逻辑推论？( )
A. 在有穷的世界里，部分可能小于整体
B. 在无穷的世界里，部分必然不等于整体
C. 在无穷的世界里，整体可能大于部分
D. 在有穷的世界里，整体必定大于部分
考题
已知公差为2的正整数等差数列为an ，则该数列满足不等式7/16 ＜an/5 ＜398/9 的所有项的和为（ ）
A. 12320
B. 12430
C. 12432
D. 12543
考题
已知数列{an｝中，Sn是它的前n项和，并且Sn+1=4an+2,a1=1．
(Ⅰ)设bn=an+1-2an，求证：数列{bn)是等比数列；
(Ⅱ)设求证：数列{cn}是等差数列；
(Ⅲ)求数列｛an｝的通项公式及前n项和．
考题
已知数列{an}的通项公式为an=2n,数列{bn}的通项公式为bn=3n+2.若数列{an}和{bn}的公共项顺序组成数列{cn},则数列{cn}的前3项之和为（ ）A.248
B.168
C.128
D.19
E.以上选项均不正确
考题
已知数列{an}的前n项和是Sn，且2Sn+an=1(n∈N*)。
(1)求证：数列{an}是等比数列；
(2)记bn=10+log9an，求{bn}的前n项和Tn的最大值及相应的n值。
考题
在移动平均中，设移动n年则（）。A、当n为偶数时，移动后所得新数列较原数列首尾各缺n∕2项B、当n为奇数时，移动后所得新数列较原数列首尾缺（N-1）∕2项C、当n为偶数时，移动后所得新数列较原数列首尾缺n项D、当n为奇数时，移动后所得新数列较原数列首尾缺n项
考题
问答题在考生文件夹下有一个工程文件sjt5.vbp。其功能是产生并显示一个数列的前n项。数列产生的规律是：数列的前2项是小于10的正整数，将此两数相乘，若乘积10，则以此乘积作为数列的第3项，若乘积≥10，则以乘积的十位数为数列的第3项，以乘积的个位数为数列的第4项。再用数列的最后两项相乘，用上述规则形成后面的项，直至产生了第n项。窗体上部从左到右3个文本框的名称分别为Text1、Text2、Text3，窗体下部的文本框名称为Text4。程序运行时，在Text1、Text2中输入数列的前两项，Text3中输入要产生的项数n，单击“计算”按钮则产生此数列的前n项，并显示在Text4中。如下图所示。 程序提供代码 已经给出了全部控件，但程序不完整，请去掉程序中的注释符，把程序中的“?”改为正确的内容。 注意：不得修改原有程序和控件的属性。最后把修改后的文件按原文件名存盘。
考题
单选题已知数列{an}是公差为d的等差数列，Sn是其前n项和，且有S9＜S8＝S7，则下列说法中不正确的是（ ）。A
S9＜S10B
d＜0C
S7与S8均为Sn的最大值D
a8＝0
热门标签
最新试卷