网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
已知等差数列{an}中，a1=21，Sn是它的前n项之和，S7=S15。
(1)求Sn；
(2)这个数列的前多少项之和最大 求出最大值。

参考答案

参考解析
解析：(1)设等差数列的公差为d，由题意可得：



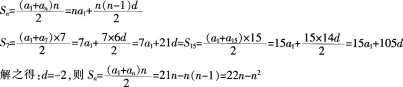
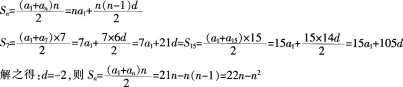
(2)Sn=22n-n2=-(n-11)2+121，当n=11时，数列之和最大，最大值为121。
更多 “已知等差数列{an}中，a1=21，Sn是它的前n项之和，S7=S15。 (1)求Sn； (2)这个数列的前多少项之和最大 求出最大值。” 相关考题
考题 已知等差数列{an}的首项与公差相等，{an）的前n项的和记作Sn，且S20=840．（I）求数列{an}的首项a1及通项公式；（Ⅱ）数列{an}的前多少项的和等于847.
查看答案
考题 已知数列{an}的前n项和Sn=n2-2n．求（I）{an}的前三项；（II）{an}的通项公式．
查看答案
考题 （19）（本题满分14分）设a1，d为实数，首项为a1，z差为d的等差数{an}的前n项和为Sn，满足S5S6＋15＝0．（Ⅰ）若S5＝5．求S6及a1;
查看答案
考题 一个等差数列，它的开始四项之和为70，最后四项之和为10，所有项的和为640，则这个数列一共有(　)项。A、56　　B、60　　C、64　　D、72
查看答案
考题 把自然数n的各位数字之和记为Sn，如n=38，Sn=3+8-11。若对某些自然数n满足n-Sn-2007．则n的最大值是()。A．2010B．2016C．2019D．2117
查看答案
考题 已知数列{an}中,a1=2,an+1=(1+an)/(1-an).记数列{an}的前n项的乘积为∏n,则∏2012=____.
查看答案
考题 一个等差数列，它的开始四项之和为70，最后四项之和为10，所有项的和为640，则这个数列一共有（ ）项。A、 56B、 60C、 64D、 72
查看答案
考题 设Sn为等差数列｛an｝的前n项和，若S3=3，S6=24，则a9= 。
查看答案
考题 在等差数列{an}中，已知a1=2，且a2+a4=20，若an=18，则n=5。()
查看答案
考题 已知一等差数列a1，21，a3，31，…，an，…，若an=516，则该数列前n项的平均数是（ ）A．266 B．258 C．255 D．212
查看答案
考题 已知等差数列前n项和 (Ⅰ)求这个数列的逋项公式； (II)求数列第六项到第十项的和．
查看答案
考题 等差数列{an)中，已知前15项之和S15＝90，则a1＋a15＝＝（　　）A.8 B.10 C.12 D.14
查看答案
考题 已知一个等差数列的第五项等于10，前三项的和等于3，那么这个等差数列的公差为（ ）A.3 B.1 C.-1 D.-3
查看答案
考题 在等比数列中，a1=3，an=96，Sn=189，则公比q=，项数n=。
查看答案
考题 已知数列{an｝中，Sn是它的前n项和，并且Sn+1=4an+2,a1=1． (Ⅰ)设bn=an+1-2an，求证：数列{bn)是等比数列； (Ⅱ)设求证：数列{cn}是等差数列； (Ⅲ)求数列｛an｝的通项公式及前n项和．
查看答案
考题 等差数列前n项和为210,其中前4项和为40,后4项的和为80,则n的值为（ ）A.10 B.12 C.14 D.16 E.18
查看答案
考题 设数列an的前n项和为Sn，则数列an是等差数列。（1）Sn=n2+2n，n=1，2，3……（2）Sn=n2+2n+1，n=1，2，3……A.条件（1）充分，但条件（2）不充分 B.条件（2）充分，但条件（1）不充分 C.条件（1）和条件（2）单独都不充分，但条件（1）和条件（2）联合起来充分 D.条件（1）充分，条件（2）充分 E.条件（1）和条件（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
查看答案
考题 已知{an）是公差大于零的等差数列，Sn是{an）的前n项和．则Sn≥S10,n=1，2，…．（1）a10=0；（2）a11a10小于0A.条件（1）充分，但条件（2）不充分； B.条件（2）充分，但条件（1）不充分； C.条件（1）和条件（2）单独都不充分，但条件（1）和条件（2）联合起来充分； D.条件（1）充分，条件（2）也充分； E.条件（1）和条件（2）单独都不充分，条件（1）和条件（7）联合起来也不充分．
查看答案
考题 已知某等差数列共有20项,其奇数项之和为30,偶数项之和为40,则其公差为（ ）.A.5 B.4 C.3 D.2 E.1
查看答案
考题 一个等差数列的前12项的和为354,前12项中偶数项之和与奇数项之和的比是32:27,则其项数为（ ）A.3 B.4 C.5 D.6 E.7
查看答案
考题 (10分)已知数列{an}满足a1=3，an+1= an +2n， (1)求{ an }的通项公式an； (2)若bn=n an，求数列{bn}的前n项和sn。
查看答案
考题 (10分)已知数列{an}的前n项和Sn=2n+1-k(其中k为常数)： (1)求数列{ an }的通项公式；(4分) (2)若a1=2，求数列{n an }的前n项和Tn。(6分)
查看答案
考题 已知数列{an}的前n项和是Sn，且2Sn+an=1(n∈N*)。 (1)求证：数列{an}是等比数列； (2)记bn=10+log9an，求{bn}的前n项和Tn的最大值及相应的n值。
查看答案
考题 单选题在等差数列{an}中，已知前15项之和S15＝90，那么a8＝（　　）．A 3B 4C 6D 12
查看答案
考题 单选题已知等差数列{an}满足a2＋a4＝4，a3＋a5＝10，则它的前10项的和S10＝（　　）。A 138B 135C 95D 23
查看答案
考题 单选题已知数列{an}满足an＋1＝an＋2，且a1＝1，那么它的通项公式an等于（　　）．A 2n－1B 2n＋1C 2n－2D 2n＋2
查看答案
考题 单选题已知数列{an}是公差为d的等差数列，Sn是其前n项和，且有S9＜S8＝S7，则下列说法中不正确的是（　　）。A S9＜S10B d＜0C S7与S8均为Sn的最大值D a8＝0
查看答案
热门标签
最新试卷