网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
“函数图象”是高中数学中很重要的知识点,通过复习所学函数模型及其图象特征.可以使学生对函数有一个较直观的把握和较形象的理解,缓解因函数语言的抽象性引起的学生的心理不适应及不自觉的排斥情绪。
(1)关于“函数图象及其应用”给出你的教学设计目标。(10分)
(2)确定教学重点、难点。(10分)
(3)设置两个教学环节(给出两个以上例题或练习题)并说明设计意图。(10分)
(1)关于“函数图象及其应用”给出你的教学设计目标。(10分)
(2)确定教学重点、难点。(10分)
(3)设置两个教学环节(给出两个以上例题或练习题)并说明设计意图。(10分)
参考答案
参考解析
解析:(1)教学目标主要有:
①通过练习的设置,从解决简单实际问题的过程中,体会函数模型的广泛适用性,贯穿理论联系实际、学以致用的观点,充分体现数学的应用价值,加强看图识图能力,激发学习兴趣,自觉自主参与课堂教学活动。②结合具体的问题,并从特殊推广到一般,领会函数与方程之间的内在联系,体验函数与方程思想、数形结合思想及等价转化思想的意义和价值。③通过对所给问题的自主探究和合作交流,理解动与静,整体与局部的辨证统一关系,发展对变量数学的认识,体会函数知识的核心作用。
(2)教学重点和难点
①教学重点:常见函数模型的图象特征和实际应用。通过课堂师生互动交流。共同完成对相关知识的系统归纳,借助多媒体课件演示,增加学生的直观体验,深化认识,突破重点。
②教学难点:利用函数图象研究方程问题的思想和方法。在教学过程中,自主探究学习,在实际问题的解决中学习将抽象的数学语言与直观的图象结合起来,充分利用这种结合,寻找解题思路,使问题化难为易、化繁为简,实现难点突破。
(3)教学环节及设计意图
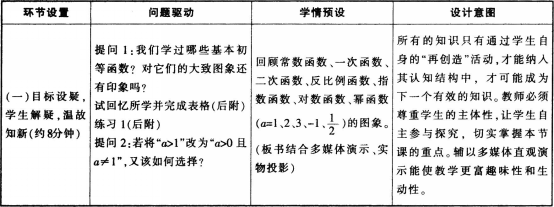

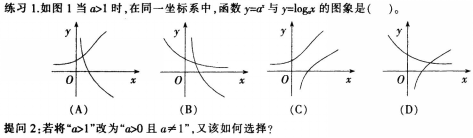



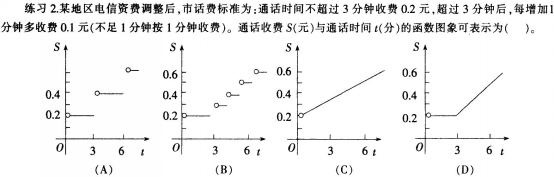


课堂小结:
本节课复习了常见函数模型及其图象特征,体会到利用函数图象解决函数性质的形象和直观。学习函数和方程的相互等价转化,体会函数方程思想与数形结合思想的意义和价值。
正如华罗庚所说:数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休。
①通过练习的设置,从解决简单实际问题的过程中,体会函数模型的广泛适用性,贯穿理论联系实际、学以致用的观点,充分体现数学的应用价值,加强看图识图能力,激发学习兴趣,自觉自主参与课堂教学活动。②结合具体的问题,并从特殊推广到一般,领会函数与方程之间的内在联系,体验函数与方程思想、数形结合思想及等价转化思想的意义和价值。③通过对所给问题的自主探究和合作交流,理解动与静,整体与局部的辨证统一关系,发展对变量数学的认识,体会函数知识的核心作用。
(2)教学重点和难点
①教学重点:常见函数模型的图象特征和实际应用。通过课堂师生互动交流。共同完成对相关知识的系统归纳,借助多媒体课件演示,增加学生的直观体验,深化认识,突破重点。
②教学难点:利用函数图象研究方程问题的思想和方法。在教学过程中,自主探究学习,在实际问题的解决中学习将抽象的数学语言与直观的图象结合起来,充分利用这种结合,寻找解题思路,使问题化难为易、化繁为简,实现难点突破。
(3)教学环节及设计意图









课堂小结:
本节课复习了常见函数模型及其图象特征,体会到利用函数图象解决函数性质的形象和直观。学习函数和方程的相互等价转化,体会函数方程思想与数形结合思想的意义和价值。
正如华罗庚所说:数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休。
更多 ““函数图象”是高中数学中很重要的知识点,通过复习所学函数模型及其图象特征.可以使学生对函数有一个较直观的把握和较形象的理解,缓解因函数语言的抽象性引起的学生的心理不适应及不自觉的排斥情绪。 (1)关于“函数图象及其应用”给出你的教学设计目标。(10分) (2)确定教学重点、难点。(10分) (3)设置两个教学环节(给出两个以上例题或练习题)并说明设计意图。(10分)” 相关考题
考题
在同一直角坐标系内一次作出函数y=x+1,y=2x+1,y=3x+1的图象。(1)这几个图象之间有什么差别,又有什么联系?(2)一次函数y=kx+b的一次项系数k对函数的图象有什么影响?
考题
学生记录由学号和成绩组成,N名学生的数据已放入主函数中的结构体数组中,请编写函数fun,其功能是:把分数最低的学生数据放入b所指的数组中,注意:分数最低的学生可能不止一个,函数返回分数最低的学生人数:注意:部分源程序在文件PROGl.C中。请勿改动主函数main和其他函数中的任何内容,仅在函数flm的花括号中填入你编写的若干语句。
考题
已知学生的记录由学号和学习成绩构成,N名学生的数据已存入a结构体数组中。请编写函数fun,函数的功能是:找出成绩最低的学生记录,通过形参返回主函数(规定只有一个最低分)。注意:部分源程序存在文件PROGl.C文件中。请勿改动主函数main和其他函数中的任何内容,仅在函数fun的莅括号中填入你编写的若干语句。
考题
已知一次函数的图象经过点A(2,1),B(-1,-3)(1)求此一次函数的解析式;(2)求此一次函数的图象与x轴、y轴的交点坐标;(3)求此一次函数的图象与两坐标轴所围成的三角形面积。
考题
A.常数k<-1
B.函数f(x)在定义域范围内,y随着x的增大而减小
C.若点C(-1,m),点B(2,n),在函数f(x)的图象上,则m<n
D.函数f(x)图象对称轴的直线方程是y=x
考题
下图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
(1)求出图象与戈轴的交点A,B的坐标;
存在,请说明理由;
° (3)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.
考题
定义[a,b,c]为函数y=ax2+bc+c的特征数,下面给出特征数为[ 2m ,1-m,-1-m]的函数的一些结论:
①当m=-3时,函数图象的顶点坐标是{1/3,-(8/3)};
②当m>0时,函数图象截石轴所得的线段长度大于3/2;
③当m1/4时,y随x的增大而减小;
④当m≠0时,函数图象经过同一个点。
其中正确的结论有()。
A.②③④
B.①②④
C.③④
D.②④
考题
初中数学《二次函数的图象与性质》
一、考题回顾
题目来源:5月18日 上午 湖北省黄石市 面试考题
试讲题目
1.题目:二次函数的图象与性质
2.内容:
3.基本要求:
(1)掌握五点作图法的画图方法,能根据图象理解二次函数的性质;
(2)试讲十分钟;
(3)要有合适的板书。
答辩题目
1.二次函数 的顶点坐标如何表示?
2.确定二次函数的表达式需要几个条件?
考题
案例:
某教师关于“反比例函数图象”教学过程中的三个步骤为:
第一步:复习回顾
提出问题:我们已经学过一次函数的哪些内容 是如何研究的
第二步:引入新课。
提出问题:反比例函数的图象是什么形状呢
引导学生利用描点法画出y=1/2的图象。
列表:
描点:
连线:引导学生用光滑的曲线连接描点,并用计算机演示图象的生成过程。在此过程中启发学生思考,由于X,Y都不能为0,所以函数图象与X轴、Y轴不能有交点(如下图)
……(第三步过程省略)
(1)该教学过程的主要特点是什么 (8分)
(2)在第二步的连线过程中,如果你是该老师,如何引导学生思考所连的线不是直线,而是光滑曲线(6分)
(3)对于第三步的③,如果你是该老师,如何引导学生思考函数图象在第一象限(或第三象限)的变化 (6分)
考题
初中“反比例函数及其图象”设定的教学目标如下:
①理解反比例函数,并能从实际问题中抽象出反比例关系的函数解析式;
⑦会画出反比例函数的图象,并结合图象分析总结出反比侧函数的性质;
③渗透数形结合的数学思想及普遍联系的辨证唯物主义思想;
④体会数学从实践中来又到实际中去的研究、应用过程;
⑤培养学生的观察能力,及数学地发现问题,解决问题的能力。
完成下列任务:
(1)根据教学目标,给出至少两个实例,并说明设计意图;(6分)
(2)本节课的教学重点是什么 (6分)
(3)作为初中阶段的基础内容,其难点是什么 (6分)
(4)请设计一个教学导入。(6分)
(5)请设计本节课小结.(6分)
考题
某教师关于“反比例函数图象”教学过程中的三个步骤为:
第一步:复习回顾
提出问题:我们已经学过一次函数的哪些内容?是如何研究的?
第二步:引入新课。
提出问题:反比例函数的图形是什么形状呢?
引导学生利用描点法画出y=1/x的图象。
列表:
描点:
连线:引导学生用光滑的曲线连接描点,并用计算机演示图象的生成过程。在此过程中启发学生思考,由于x,y都不能为0,所以函数图象与x轴、y轴不能有交点(如下图)
……(第三步过程省略)
(1)该教学过程的主要特点是什么?
(2)在第二步的连线过程中,如果你是该老师,如何引导学生思考所连的线不是直线,而是光滑曲线
(3)对于第三步的③,如果你是该老师,如何引导学生思考函数图象在第一象限(或第三象限)的变化?
考题
用户定义函数“stuinfo(参数)”功能是根据输入学生的学号,通过SELECT命令查询得到学生姓名及各科成绩,该函数属于()。A、标量函数B、内嵌表值函数C、多语句表值函数D、字符函数
考题
单选题用户定义函数“stuinfo(参数)”功能是根据输入学生的学号,通过SELECT命令查询得到学生姓名及各科成绩,该函数属于()。A
标量函数B
内嵌表值函数C
多语句表值函数D
字符函数
热门标签
最新试卷