网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设D是曲线y=x2与y=1 所围闭区域,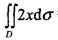 等于( )。
等于( )。
A. 1 B. 1/2 C.0 D. 2
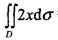 等于( )。
等于( )。
A. 1 B. 1/2 C.0 D. 2
参考答案
参考解析
解析:提示: 或积分区域关于y轴对称,被积函数关于x为奇函数,积分为零。
或积分区域关于y轴对称,被积函数关于x为奇函数,积分为零。
 或积分区域关于y轴对称,被积函数关于x为奇函数,积分为零。
或积分区域关于y轴对称,被积函数关于x为奇函数,积分为零。
更多 “设D是曲线y=x2与y=1 所围闭区域,等于( )。 A. 1 B. 1/2 C.0 D. 2” 相关考题
考题
设曲线y=f(x)上任一点(x,y)处的切线斜率为(y/x)+x2,且该曲线经过点(1,1/2)。(1)求函数y=f(x);(2)求由曲线y= f(x),y=O,x=1所围图形绕x轴旋转一周所得旋转体的体积V。
考题
设(X,Y)在由直线y=x,y=2-x,y=0所围的区域内服从均匀分布,则P{0.1
热门标签
最新试卷