网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
设随机变量X的概率密度为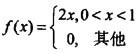
，用Y表示对X的3次独立重复观察中事件
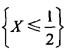出现的次数，则P{Y=2}=( )。
A.3/64 B.9/64 C.3/16 D. 9/16
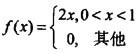，用Y表示对X的3次独立重复观察中事件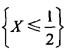出现的次数，则P{Y=2}=( )。
A.3/64 B.9/64 C.3/16 D. 9/16
参考答案
参考解析
解析：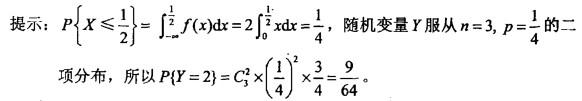
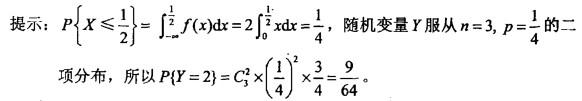
更多 “设随机变量X的概率密度为，用Y表示对X的3次独立重复观察中事件出现的次数，则P{Y=2}=( )。 A.3/64 B.9/64 C.3/16 D. 9/16” 相关考题
考题
设随机变量X与Y相互独立，X服从参数为1的指数分布，Y的概率分布为P{Y=-1}=p，P{Y=1)=1-p，(0 (Ⅰ)求Z的概率密度；
(Ⅱ)p为何值时，X与Z不相关；
(Ⅲ)X与Z是否相互独立？
考题
单选题设随机变量X的概率密度函数f（x）＝1/[π（1＋x2）]，则Y＝3X的概率密度函数为（ ）。A
1/[π（1＋y2）]B
3/[π（9＋y2）]C
9/[π（9＋y2）]D
27/[π（9＋y2）]
考题
问答题设随机变量(X,Y)的概率密度为 求：(1)系数k. (2)边缘概率密度fX(x),fY(y). (3)P{X+Y1}.
热门标签
最新试卷