网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
设随机变量X,y相互独立,且X～
,Y～E(4),令U=X+2Y,求U的概率密度.
,Y～E(4),令U=X+2Y,求U的概率密度.参考答案
参考解析
解析：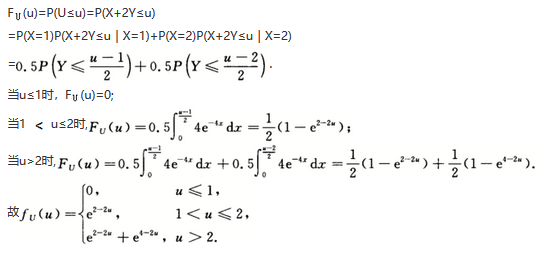
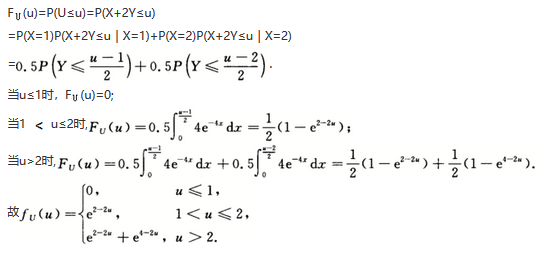
更多 “设随机变量X,y相互独立,且X～,Y～E(4),令U=X+2Y,求U的概率密度.” 相关考题
考题
设二维随机变量(X,Y)的联合密度函数为f(x,y)=
(1)求随机变量X,Y的边缘密度函数；
(2)判断随机变量X,Y是否相互独立；
(3)求随机变量Z=X+2Y的分布函数和密度函数.
考题
设随机变量X,y独立同分布,且X～N（0,σ^2）,再设U=aX+by,V=aX-bY,其中a,b为不相等的常数.求：
(1)E(U),E(V),D(U),D(V),;
(2)设U,V不相关,求常数A,B之间的关系.
考题
设随机变量X,Y独立同分布,且P(X=i)=,i=1,2,3.
设随机变量U=max{X,Y},V=min{X,Y}.
(1)求二维随机变量(U,V)的联合分布；(2)求Z=UV的分布；
(3)判断U,V是否相互独立？(4)求P（U=V）.
考题
问答题 设X与Y相互独立,X的概率密度为 Y的概率密度为 求：(1)E(2X-3Y+1),D(2X-3Y+1); (2)Cov(X,Y)，ρXY.
热门标签
最新试卷