网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
圆周ρ=cosθ,ρ=2cosθ及射线θ=0,θ=π/4所围图形的面积S为( )。


参考答案
参考解析
解析:提示:
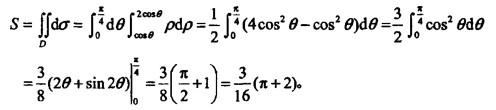
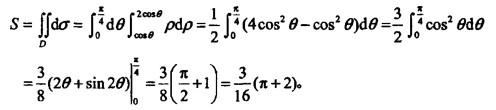
更多 “圆周ρ=cosθ,ρ=2cosθ及射线θ=0,θ=π/4所围图形的面积S为( )。 ” 相关考题
考题
已知向量OA→=(-2,0),OB→=(2,2),BC→=(2cosθ,2sinθ)(0 ≤θ
已知向量OA→=(-2,0),OB→=(2,2),BC→=(2cosθ,2sinθ)(0 ≤θ(A)[7π/6 ,11π/6].(B)[7π/12 ,11π/12].(C)[2π/3 ,5π/3].(D)[5π/4 ,7π/4].
考题
图示机构中,曲柄OA=r,以常角速度ω转动,则滑动机构BC的速度、加速度的表达式为( )。
A.rωsinωt,rωcosωt
B.rωcosωt,rω2sinωt
C.rsinωt,rωcosωt
D.rωsinωt,rω2cosωt
考题
已知向量a=(3cosα,3sinα),b=(2cosβ,2sinβ),若a与b的夹角为60°,则直线
与圆(X-cosβ)2+(Y-sinβ)2=1的位置关系是( )。A.相交且不过圆心
B.相交且过圆心
C.相切
D.相离
考题
三相四线有功电能表第一元件:Ua、Ic,第二元件:Ub、Ia,第三元件:Uc、Ib,其有功为功率为()A、P=3UI(–1/2cosφ+√3/2sinφ)B、P=0C、P=1D、P=√3UI(–1/2cosφ+√3/2sinφ)
考题
多普勒效应公式中的频移(fd)是()A、fd=f0C/2VcosθB、fd=2cosθf0/VC、fd=2f0Vcosθ/CD、fd=Cf0cosθ/2VE、fd=2CV/f0cosθ
考题
成形铣刀铣外花键时若对刀不准,会使键侧左比键侧右高ΔX,则应使键侧左向铣刀靠拢一个距离S,则S等于()。A、ΔX/cos(180°/Z)B、ΔX/2cos(180°/Z)C、ΔX/sin(180°/Z)D、2ΔX/sin(180°/Z)
考题
波长为λ、向右传播的某简谐波,其波源的振动方程为x=2cosπt,则传播方向上与波源相距一个波长的质点振动方程为:()A、x=2cos(πt-π)B、x=2cos(πt-2π)C、x=2cosπtD、x=2cos(πt+2π)
考题
功率因数由cosφ1提高到cosφ2,设备节省容量ΔS为()。A、ΔS=P(1/cosφ1-1/cosφ2)B、ΔS=Q(1/cosφ1-1/cosφ2)C、ΔS=P(tanφ1-tanφ2)D、ΔS=Q(tanφ1-tanφ2)
考题
单选题(6sin x) (3sin x)-(9cos x) (-2cos x) = ______.A
1B
-18C
18D
-1E
18sin2x-18cos2x
热门标签
最新试卷