网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
已知三阶方阵A,B满足关系式E+B=AB,A的三个特征值分别为3,-3,0,则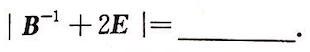
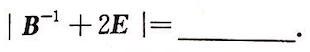
参考答案
参考解析
解析:因为A的特征值为3,-3,0,所以A-E的特征值为2,-4,-1,从而A-E可逆。由E+B=AB得(A-E)B=E,即B与A-E互为矩阵,则B的特征值为
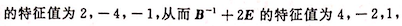
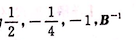
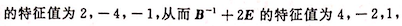
更多 “已知三阶方阵A,B满足关系式E+B=AB,A的三个特征值分别为3,-3,0,则” 相关考题
考题
下列命题不正确的是()
A、转置运算不改变方阵A的行列式值和秩B、若mC、已知同阶方阵A,B和C满足AB=AC,若A是非奇异阵,则B=CD、若矩阵A的列向量线性相关,则A的行向量也线性相关
考题
设A,B均为n阶方阵,则()
A、若|A+AB|=0,则|A|=0或|E+B|=0B、(A+B)^2=A^2+2AB+B^2C、当AB=O时,有A=O或B=OD、(AB)^-1=B^-1A^-1
考题
已知三维列向量αβ满足αTβ=3,设3阶矩阵A=βαT,则:
A. β是A的属于特征值0的特征向量
B. α是A的属于特征值0的特征向量
C. β是A的属于特征值3的特征向量
D. α是A的属于特征值3的特征向量
考题
已知三维列向量a,β满足aTβ,设3阶矩阵A=βaT,则:
A. β是A的属于特征值0的特征向量
B. a是A的属于特征值0的特征向量
C. β是A的属于特征值3的特征向量
D. a是A的属于特征值3的特征向量
考题
已知3维列向量α,β满足αTβ=3,设3阶矩阵A=βαT,则()。A、β是A的属于特征值0的特征向量B、α是A的属于特征值0的特征向量C、β是A的属于特征值3的特征向量D、α是A的属于特征值3的特征向量
考题
单选题已知3维列向量α,β满足αTβ=3,设3阶矩阵A=βαT,则()。A
β是A的属于特征值0的特征向量B
α是A的属于特征值0的特征向量C
β是A的属于特征值3的特征向量D
α是A的属于特征值3的特征向量
考题
单选题设A为3阶方阵,α(→)1,α(→)2,α(→)3是互不相同的3维列向量,且都不是方程组Ax(→)=0(→)的解,若B=(α(→)1,α(→)2,α(→)3)满足r(AB)<r(A),r(AB)<r(B),则r(AB)等于( )。A
3B
2C
1D
0
考题
问答题设有三个非零的n阶(n≥3)方阵A1、A2、A3,满足Ai2=Ai(i=1,2,3),且AiAj=0(i≠j,i、j=1,2,3),证明: (1)Ai(i=1,2,3)的特征值有且仅有0和1; (2)Ai的对应于特征值1的特征向量是Aj的对应于特征值0的特征向量(i≠j); (3)若α(→)1、α(→)2、α(→)3分别为A1、A2、A3的对应于特征值1的特征向量,则向量组α(→)1、α(→)2、α(→)3线性无关。
热门标签
最新试卷