网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
根据图1所示AB、CD直线和P、Q平面,选择回答如下题:
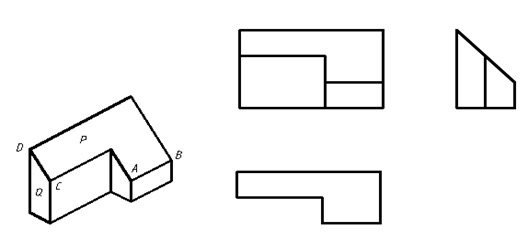
1.AB、CD直线的正面投影应标记为()。
A.a’b’、c’d’
B.a”b”、c”d”
C.ab、cd
D.AB、CD
2.AB、CD直线的水平投影应标记为()。
A.a’b’、c’d’
B.a”b”、c”d”
C.AB、CD
D.ab、cd
3.P、Q平面的正面投影应标记为()。
A.P、Q
B.p’、q’
C.p、q
D.p”、q”
4.P、Q平面的水平投影应标记为()。
A.p’、q’
B.p”、q”
C.p、q
D.P、Q
5.P、Q平面的侧面投影应标记为()。
A.p’、q’
B.P、Q
C.p、q
D.p”、q”
参考答案
更多 “ 根据图1所示AB、CD直线和P、Q平面,选择回答如下题:1.AB、CD直线的正面投影应标记为()。A.a’b’、c’d’B.a”b”、c”d”C.ab、cdD.AB、CD2.AB、CD直线的水平投影应标记为()。A.a’b’、c’d’B.a”b”、c”d”C.AB、CDD.ab、cd3.P、Q平面的正面投影应标记为()。A.P、QB.p’、q’C.p、qD.p”、q”4.P、Q平面的水平投影应标记为()。A.p’、q’B.p”、q”C.p、qD.P、Q5.P、Q平面的侧面投影应标记为()。A.p’、q’B.P、QC.p、qD.p”、q” ” 相关考题
考题
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90o,E是CD的中点。
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。
考题
假设平面P为水平面,平面Q为一般位置平面,关于它们的交线AB,下列说法正确的是()。A.AB在V和W面内的投影在同一条直线上B.AB在V和H面内的投影在同一条直线上C.AB在H和W面内的投影在同一条直线上D.所有说法都不正确
考题
假设平面P为水平面,平面Q为一般位置平面,关于它们的交线AB,下列说法正确的是()。A.AB的三面投影均为直线B.AB在V和H面内的投影可能在同一条直线上C.AB在V和W面内的投影可能在同一条直线上D.AB在W和H面内的投影可能在同一条直线上E.不可能出现AB的两个投影在同一条直线上的情况
考题
假设空间中的直线AB和CD平行,则下列说法正确的是()。A.AB和CD在某个投影面内的投影可能积聚成为同一个点B.AB和CD在某个投影面内的投影可能积聚成为同一条直线C.AB和CD在三个投影面内的投影可能均相互平行D.AB和CD在任意投影面内的投影都不可能积聚成为同一个点
考题
当平面平行于投影面时,平面在该投影面上的投影: A:反映实形 B:集聚为一条直线 C:为原平面形的类似形 D:集聚为一条曲线A.AB.BC.CD.D
热门标签
最新试卷