网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
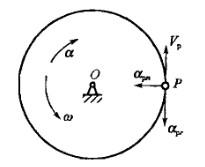
半径r的圆盘以其圆心O为轴转动,角速度ω,角加速度为a。盘缘上点P的速度VP,切向加速度apr与法向加速度apn的方向如图,它们的大小分别为:
A. vp=rω,aPr=ra,aPn =rω2 B. vp = rω,aPr=ra2 ,apn=r2ω
C. vp=r/ω,apr=ra2,apn = rω2 D. vp=r/ω,apr= ra,apn=rω2

A. vp=rω,aPr=ra,aPn =rω2 B. vp = rω,aPr=ra2 ,apn=r2ω
C. vp=r/ω,apr=ra2,apn = rω2 D. vp=r/ω,apr= ra,apn=rω2
参考答案
参考解析
解析:提示:根据定轴转动刚体上一点速度、加速度的公式。
更多 “半径r的圆盘以其圆心O为轴转动,角速度ω,角加速度为a。盘缘上点P的速度VP,切向加速度apr与法向加速度apn的方向如图,它们的大小分别为: A. vp=rω,aPr=ra,aPn =rω2 B. vp = rω,aPr=ra2 ,apn=r2ω C. vp=r/ω,apr=ra2,apn = rω2 D. vp=r/ω,apr= ra,apn=rω2” 相关考题
考题
质量为m,半径为R的均质圆轮,绕垂直于图面的水平轴O转动,其角速度为w。在图示瞬时,角加速度为0,轮心C在其最低位置,此时将圆轮的惯性力系向O点简化, 其惯性力主矢和惯性力主矩的大小分别为:
考题
杆OA绕固定轴O转动,圆盘绕动轴A转动,已知杆长l=20cm,圆盘r=10cm,在图示位置时,杆的角速度及角加速度分别为w=4rad/s,ε=3rad/s2;圆盘相对于OA的角速度和角加速度分别为wr=6rad/s,εr=4rad/s2。则圆盘上M1点绝对加速度为( )。
A.a1=363cm/s2
B.a1=463cm/s2
C.a1=563cm/s2
D.a1=663cm/s2
考题
质量为m,半径为R的均质圆轮,绕垂直于图面的水平轴O转动,其角速度为w。在图示瞬时,角加速度为O,轮心C在其最低位置,此时将圆轮的惯性力系向O点简化,其惯性力主矢和惯性力主矩的大小分别为:
考题
质量为m,半径为R的均质圆盘,绕垂直于图面的水平轴O转动,其角速度为ω,在图示瞬时,角加速度为零,盘心C在其最低位置,此时将圆盘的惯性力系向O点简化, 其惯性力主矢和惯性力主矩的大小分别为:
考题
圆盘某瞬时以角速度ω,角加速度α绕O轴转动,其上A、B两点的加速度分别为aA和aB,与半径的夹角分别为θ和φ。若OA=R,OB=R/2,则aA与aB,θ与φ的关系分别为:
A.aA=aB,θ=φ
B. aA=aB,θ=2φ
C. aA=2aB,θ=φ
D. aA=2aB,θ=2φ
考题
质量为m,半径为R的均质圆盘,绕垂直于图面的水平轴O转动,其角速度为ω,在图4-78示瞬时,角加速度为零,盘心C在其最低位置,此时将圆盘的惯性力系向O点简化,其惯性力主矢和惯性力主矩的大小分别为()。
考题
如图4-45所示,圆盘某瞬时以角速度ω,角加速度α绕轴O转动,其上A、B两点的加速度分别为aA和aB,与半径的夹角分别为θ和φ。若OA=R, OB = R/2,则aA与aB,θ与 φ 的关系分别为( )。
A.aA=aB θ=φ B.aA=aB θ=2φ C.aA=2aB θ=φ D.aA=2aB θ=2φ
考题
单选题某瞬时刚体的转动方向是指()。A
瞬时角速度方向B
瞬时角加速度方向C
切向加速度方向D
法向加速度方向
热门标签
最新试卷