网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
微分方程(1+y)dx-(1-x)dy=0的通解是(c为任意常数)：
参考答案
参考解析
解析：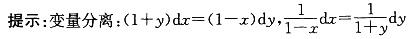
积分得：ln(1-x)+ln(1+y)=lnc。
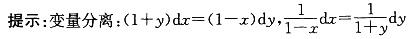积分得：ln(1-x)+ln(1+y)=lnc。
更多 “微分方程(1+y)dx-(1-x)dy=0的通解是(c为任意常数)： ” 相关考题
考题
下列一阶微分方程中，哪一个是一阶线性方程（）？A、（xey-2y）dy+eydx=0B、xy′+y=ex+yC、［x／（1+y）]dx-[y／（1+x）］dy=0D、dy／dx=（x+y）／（x-y）
考题
单选题（2012）已知微分方程y′+p+（x）y=q（x）［q（x）≠0］有两个不同的特解y1（x），y2（x），则该微分方程的通解是：（c为任意常数）（）A
y=c（y1-y2）B
y=c（y1+y2）C
y=y1+c（y1+y2）D
y=y1+c（y1-y2）
考题
单选题设y＝ex（c1sinx＋c2cosx）（c1、c2为任意常数）为某二阶常系数线性齐次微分方程的通解，则该方程为（ ）。A
y″－y′＋y＝0B
y″－2y′＋2y＝0C
y″－2y′＝0D
y′＋2y＝0
考题
单选题在下列微分方程中，以y＝C1ex＋C2cos2x＋C3sin2x（C1，C2，C3为任意常数）为通解的是（ ）。A
y‴＋y″－4y′－4y＝0B
y‴＋y″＋4y′＋4y＝0C
y‴－y″－4y′＋4y＝0D
y‴－y″＋4y′－4y＝0
考题
单选题下列一阶微分方程中，哪一个是一阶线性方程（）？A
（xey-2y）dy+eydx=0B
xy′+y=ex+yC
［x／（1+y）]dx-[y／（1+x）］dy=0D
dy／dx=（x+y）／（x-y）
考题
单选题已知微分方程y′+p（x）y=q（x）（q（x）≠0）有两个不同的解y1（x），y2（x），C为任意常数，则该微分方程的通解是（ ）。[2012年真题]A
y=C（y1-y2）B
y=C（y1+y2）C
y=y1+C（y1+y2）D
y=y1+C（y1-y2）
考题
单选题设y＝ex（c1sinx＋c2cosx）（c1、c2为任意常数）为某二阶常系数线性齐次微分方程的通解，则该方程为（ ）。A
y″＋2y′＋2y＝0B
y″－2y′＋2y＝0C
y″－2y′－2y＝0D
y″＋2y′＋2y＝0
热门标签
最新试卷
