网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设矩阵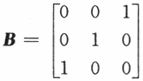 ,已知矩阵A相似于B,则秩(A-2E)与秩(A-E)之和等于
,已知矩阵A相似于B,则秩(A-2E)与秩(A-E)之和等于
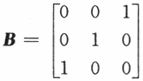 ,已知矩阵A相似于B,则秩(A-2E)与秩(A-E)之和等于
,已知矩阵A相似于B,则秩(A-2E)与秩(A-E)之和等于A.2
B.3
C.4
D.5
B.3
C.4
D.5
参考答案
参考解析
解析:

更多 “设矩阵,已知矩阵A相似于B,则秩(A-2E)与秩(A-E)之和等于A.2 B.3 C.4 D.5” 相关考题
考题
设A是S×6矩阵,则( )正确。A.若A中所有5阶子式均为0,则秩R(A)=4
B.若秩R(A)=4,则A中5阶子式均为0
C.若秩R(A)=4,则A中4阶子式均非0
D.若A中存在不为0的4阶子式,则秩尺(A)=4
考题
下列结论中正确的是( )。
A、 矩阵A的行秩与列秩可以不等
B、 秩为r的矩阵中,所有r阶子式均不为零
C、 若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零
D、 秩为r的矩阵中,不存在等于零的r-1阶子式
考题
设A为m×n矩阵,B为n×m矩阵,E为m阶单位矩阵,若AB=E,则
A.A秩r(A)=m,秩r(B)=m
B.秩r(A)=m,秩r(B)=n
C.秩r(A)=n,秩r(B)=m
D.秩r(A)=n,秩r(B)=n
考题
设A、B分别为n×m,n×l矩阵,C为以A、B为子块的n×(m+l)矩阵,即C=(A,B),则( ).《》( )A.秩(C)=秩(A)
B.秩(C)=秩(B)
C.秩(C)与秩(A)或秩(C)与秩(B)不一定相等
D.若秩(A)=秩(B)=r,则秩(C)=r
考题
单选题下列结论中正确的是( )A
矩阵A的行秩与列秩可以不等B
秩为r的矩阵中,所有r阶子式均不为零C
若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零D
秩为r的矩阵中,不存在等于零的r-1阶子式
热门标签
最新试卷