网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设A为四阶实对称矩阵,且A^2+A=O.若A的秩为3,则A相似于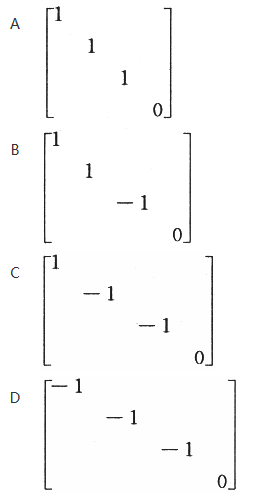

参考答案
参考解析
解析:这是一道常见的基础题,由Aα=λα,α≠0知A^nα=λ^nα,那么对于A^2+A=0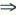 (λ^2+λ)α=0
(λ^2+λ)α=0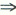 λ^2+λ=0所以A的特征值只能是0或-1再由A是实对称必有A~A,而A即是A的特征值,那么由r(A)=3,可知(D)正确
λ^2+λ=0所以A的特征值只能是0或-1再由A是实对称必有A~A,而A即是A的特征值,那么由r(A)=3,可知(D)正确
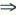 (λ^2+λ)α=0
(λ^2+λ)α=0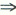 λ^2+λ=0所以A的特征值只能是0或-1再由A是实对称必有A~A,而A即是A的特征值,那么由r(A)=3,可知(D)正确
λ^2+λ=0所以A的特征值只能是0或-1再由A是实对称必有A~A,而A即是A的特征值,那么由r(A)=3,可知(D)正确
更多 “设A为四阶实对称矩阵,且A^2+A=O.若A的秩为3,则A相似于” 相关考题
考题
设A,B为n阶矩阵,考虑以下命题:①若A,B为等价矩阵,则A,B的行向量组等价②若行列式.,则A,B为等价矩阵③若与都只有零解,则A,B为等价矩阵④若A,B为相似矩阵,则与的解空间的维数相同以上命题中正确的是( ).
A.①③
B.②④
C.②③
D.③④
考题
设A为m×n矩阵,B为n×m矩阵,E为m阶单位矩阵,若AB=E,则
A.A秩r(A)=m,秩r(B)=m
B.秩r(A)=m,秩r(B)=n
C.秩r(A)=n,秩r(B)=m
D.秩r(A)=n,秩r(B)=n
考题
设A、B分别为n×m,n×l矩阵,C为以A、B为子块的n×(m+l)矩阵,即C=(A,B),则( ).《》( )A.秩(C)=秩(A)
B.秩(C)=秩(B)
C.秩(C)与秩(A)或秩(C)与秩(B)不一定相等
D.若秩(A)=秩(B)=r,则秩(C)=r
考题
单选题设3阶矩阵,已知A的伴随矩阵的秩为1,则a=()。A
-2B
-1C
1D
2
热门标签
最新试卷