网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设A为3阶实对称矩阵,A的秩为2,且.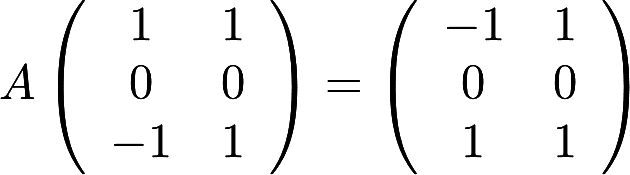 (Ⅰ)求A的特征值与特征向量; (Ⅱ)求矩阵A
(Ⅰ)求A的特征值与特征向量; (Ⅱ)求矩阵A
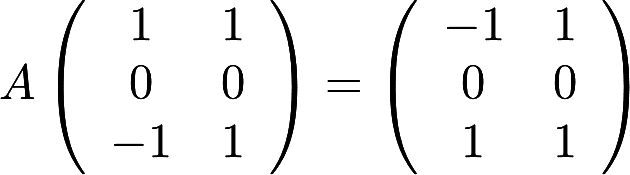 (Ⅰ)求A的特征值与特征向量; (Ⅱ)求矩阵A
(Ⅰ)求A的特征值与特征向量; (Ⅱ)求矩阵A参考答案
参考解析
解析:
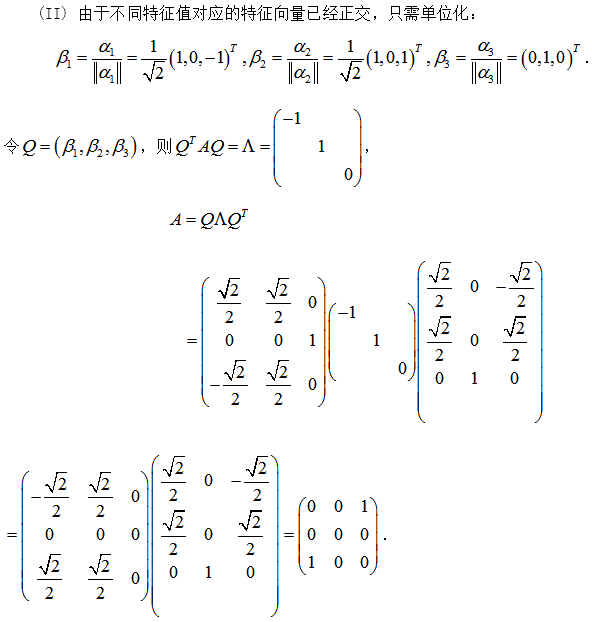

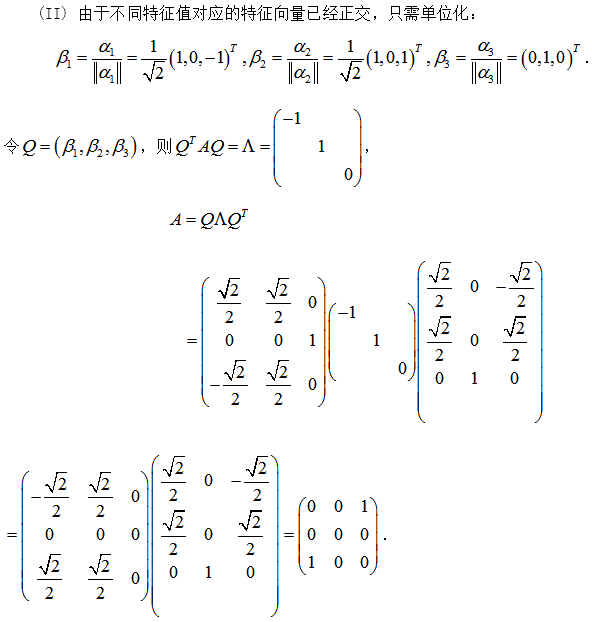
更多 “设A为3阶实对称矩阵,A的秩为2,且. (Ⅰ)求A的特征值与特征向量; (Ⅱ)求矩阵A” 相关考题
考题
设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知a是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:
A. Pa B. P-1A C. PTa D.(P-1)Ta
考题
设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知α是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:(A) Pα (B) P-1α (C) PTa (D) P(-1)Ta
考题
设n阶矩阵A可逆,α是A的属于特征值λ的特征向量,则下列结论中不正确的是()。A、α是矩阵-2A的属于特征值-2λ的特征向量B、α是矩阵的属于特征值的特征向量C、α是矩阵A*的属于特征值的特征向量D、α是矩阵AT的属于特征值λ的特征向量
考题
单选题(2009)设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知α是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:()A
PαB
P-1αC
PTαD
(P-1)Tα
热门标签
最新试卷