网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
在数列{an}(n=1,2,…)中,a1=1959,a2=1995,且从第三项起,每项是它前两项平均的整数部分,则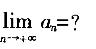
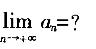
A. 1980
B.1981
C.1983
D.1982
B.1981
C.1983
D.1982
参考答案
参考解析
解析:计算数列前面几项,注意题中关键词--“前两项平均的整数部分”。1959,1995,1977,1986,1981,1983,1982,1982…,可见数列从第七项开始都是1982,故此题所求为1982。
更多 “在数列{an}(n=1,2,…)中,a1=1959,a2=1995,且从第三项起,每项是它前两项平均的整数部分,则 A. 1980 B.1981 C.1983 D.1982 ” 相关考题
考题
请在函数fun()的横线上填写若干表达式,使从键盘上输入一个整数n,输出n对应的斐波那契数列。斐波那契数列是一整数数列,该数列自第三项开始,每数等于前面两数之和,即0,1,1,2,3,5,8,13,21,34,55,…。注意:部分源程序给出如下。请勿改动主函数main和其他函数中的任何内容,仅在函数fun()的横线上填入所编写的若干表达式或语句。试题程序:include<stdio.h>int fun(int n);main(){int i,n=0;scanf("%d",n);for(i=0;i<n; i++)printf("%d",fun(i));}int fun(int n){if(【 】)return 0;elseif(【 】)return 1;elsereturn【 】;}
考题
Fibonacci(斐波那契)数列是一个非常著名的数列,它在计算机科学等许多领域都有重要的应用,甚至,在预测商品价格和证券价格时也能见到其踪影。现已知该数列的第一项和第二项均为1,从第三项起每项均为其前面最近相邻两项的和。请编写程序输出该数列的前40项,每行输出4项。注意:编程语言不限,如C/C++、JAVA、PASCAL甚至VFP均可。
考题
从满足a1=a2=1,an+2=an+1+an(n≥1)的数列{an)中,依次抽出能被3整除的项组成数列{bn},则b100是多少? A.a100 B.a200 C.a300 D.a400
考题
请在函数proc()的横线上填写若干表达式,使从键盘上输入一个整数n,输出斐波那契数列的前n个数。斐波那契数列是一个整数数列,该数列自第3项开始,每个数等于前面两个数之和,即0,1,1,2,3,5,8,13,21,34,55,…注意:部分源程序给出如下。请勿改动main()函数和其他函数中的任何内容,仅在函数proc()的横线上填入所编写的若干表达式或语句。试题程序:
考题
设Xi(i=1,2,…,n)为n个相互独立的随机变量,则下列结论成立的是( )。A.若Xi(i=1,2,…,n)服从正态分布,且分布参数相同,则服从正态分布B.若Xi(i=1,2,…,n)服从指数分布,且λ相同,则服从正态分布C.若Xi(i=1,2,…,n)服从[a,b]上的均匀分布,则服从正态分布D.无论Xi(i=1,2,…,n)服从何种相同的分布,其均值都服从正态分布
考题
设Xi (i=1,2,…,n)为n个相互独立的随机变量,则下列结论成立的是( )。A.若Xi (i=1,2,…,n)服从正态分布,且分布参数相同,则服从正态分布B.若Xi (i=1,2,…,n)服从指数分布,且λ相同,则服从正态分布C.若Xi(i=1,2,…,n)服从[a,b)上的均匀分布,则服从正态分布D.无论Xi (i=1,2,…,n)服从何种分布,其均值都服从正态分布
考题
在代数系统中,T为m,n 间的整数集合,m
在代数系统<T,min>中,T为m,n 间的整数集合,m<n,且T 包括m 和n,min为两个整数中取小者的运算,则T中存在逆元的元素有(58)。A.mB.nC.D.没有存在逆元的元素
考题
阅读说明和流程图,填补流程图中的空缺(1)?(5),将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1,a2=1,…,an=an-1+an-2!n=3,4,…}的前n项(n>=2) 之和S。例如,菲波那契数列前6项之和为20。计算过程中,当前项之前的两项分别动态地保存在变量A和B中。【流程图】
考题
已知数列{an}中,Sn是它的前n项和,并且Sn+1=4an+2,a1=1.
(Ⅰ)设bn=an+1-2an,求证:数列{bn)是等比数列;
(Ⅱ)设求证:数列{cn}是等差数列;
(Ⅲ)求数列{an}的通项公式及前n项和.
考题
已知{an}是由非负整数组成的无穷数列,该数列前n项的最大值记为A。第项之后各
(1)若是一个周期为4的数列(即对任意写出dl,dz,d3,d0的值;
(2)设d为非负整数,证明:do=一d(n=1,2,3…)的充分必要条件为{an}为公差为d的等差数列:
(3)证明:若a1=2,dn=1(n=1,2,3,…),则{an}的项只能是1或者2,且有无穷多项为l。
考题
设{an}为数列,对于“存在正数肘,对任意正整数n,有
的否定(即数列{an}无界)是( )。
A、存在正数M,存在正整数n,使得|an|>M
B、对任意正数M,存在正整数n,使得|an|>M
C、存在正数M,对任意正整数n,有|an|>M
D、对任意正数M以及任意正整数n,有|an|>M
考题
已知数列{an}的前n项和是Sn,且2Sn+an=1(n∈N*)。
(1)求证:数列{an}是等比数列;
(2)记bn=10+log9an,求{bn}的前n项和Tn的最大值及相应的n值。
考题
在移动平均中,设移动n年则()。A、当n为偶数时,移动后所得新数列较原数列首尾各缺n∕2项B、当n为奇数时,移动后所得新数列较原数列首尾缺(N-1)∕2项C、当n为偶数时,移动后所得新数列较原数列首尾缺n项D、当n为奇数时,移动后所得新数列较原数列首尾缺n项
考题
问答题在考生文件夹下有一个工程文件sjt5.vbp。其功能是产生并显示一个数列的前n项。数列产生的规律是:数列的前2项是小于10的正整数,将此两数相乘,若乘积10,则以此乘积作为数列的第3项,若乘积≥10,则以乘积的十位数为数列的第3项,以乘积的个位数为数列的第4项。再用数列的最后两项相乘,用上述规则形成后面的项,直至产生了第n项。窗体上部从左到右3个文本框的名称分别为Text1、Text2、Text3,窗体下部的文本框名称为Text4。程序运行时,在Text1、Text2中输入数列的前两项,Text3中输入要产生的项数n,单击“计算”按钮则产生此数列的前n项,并显示在Text4中。如下图所示。 程序提供代码 已经给出了全部控件,但程序不完整,请去掉程序中的注释符,把程序中的“?”改为正确的内容。 注意:不得修改原有程序和控件的属性。最后把修改后的文件按原文件名存盘。
考题
单选题以下是斐波那契数列特点的是()A
只有第一项为1B
第三项起,每一项是前两项之和C
相邻两项的差相等D
相邻两项的比相等
热门标签
最新试卷