网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
已知矩阵 .
.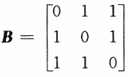 ,且矩阵X满足AXA+BXB=AXB+BXA+E,其中E是三阶单位矩阵,求X.
,且矩阵X满足AXA+BXB=AXB+BXA+E,其中E是三阶单位矩阵,求X.
 .
.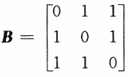 ,且矩阵X满足AXA+BXB=AXB+BXA+E,其中E是三阶单位矩阵,求X.
,且矩阵X满足AXA+BXB=AXB+BXA+E,其中E是三阶单位矩阵,求X.参考答案
参考解析
解析:【解】化简矩阵方程,有AX(A-B)+BX(B-A)=E,即(A-B)X(A-B)=E.
由于 ,所以矩阵A-B可逆,且
,所以矩阵A-B可逆,且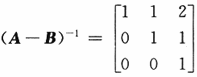 于是.
于是.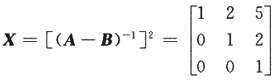
由于
 ,所以矩阵A-B可逆,且
,所以矩阵A-B可逆,且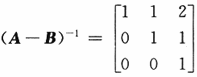 于是.
于是.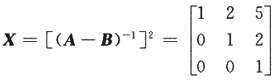
更多 “已知矩阵.,且矩阵X满足AXA+BXB=AXB+BXA+E,其中E是三阶单位矩阵,求X.” 相关考题
考题
设A是m×n矩阵,B是n×m矩阵,且AB=E,其中E为m阶单位矩阵,则( )
A.r(A)=r(B)=m
B.r(A)=m r(B)=n
C.r(A)=n r(B)=m
D.r(A)=r(B)=n
考题
问答题设A是n阶矩阵,且满足Am=E,其中m为整数,E为n阶单位矩阵。令将A中的元素aij换成它的代数余子式Aij而成的矩阵为A(~),证明:(A(~))m=E。
热门标签
最新试卷