网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.

参考答案

参考解析
解析：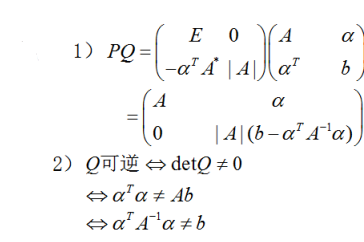
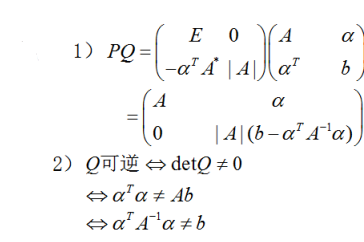
更多 “设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.” 相关考题
考题 设A为n阶对称矩阵,则A是正定矩阵的充分必要条件是( ). A.二次型xTAx的负惯性指数零B.存在n阶矩阵C,使得A=CTCC.A没有负特征值D.A与单位矩阵合同
查看答案
考题 设A为n阶可逆矩阵，则(-A)的伴随矩阵(-A)*等于( )。 A.-A.* B.A.* C.(-1)nA.* D.(-1)n-1A.*
查看答案
考题 与n阶单位矩阵E相似的矩阵是 A. B.对角矩阵D（主对角元素不为1） C.单位矩阵E D.任意n阶矩阵A
查看答案
考题 设n阶矩阵A与对角矩阵相似,则().A.A的n个特征值都是单值 B.A是可逆矩阵 C.A存在n个线性无关的特征向量 D.A一定为n阶实对称矩阵
查看答案
考题 设A为m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r1，矩阵B=AC的秩为r，则
查看答案
考题 设A是m×n矩阵，B是n×m矩阵，且AB=E,其中E为m阶单位矩阵，则（ ） A.r(A)=r(B)=m B.r(A)=m r(B)=n C.r(A)=n r(B)=m D.r(A)=r(B)=n
查看答案
考题 设A为n阶实对称矩阵,下列结论不正确的是().A.矩阵A与单位矩阵E合同 B.矩阵A的特征值都是实数 C.存在可逆矩阵P,使P^-1AP为对角阵 D.存在正交阵Q,使Q^TAQ为对角阵
查看答案
考题 设A为n阶矩阵,证明：r(A)=1的充分必要条件是存在n维非零列向量α,β使得A=αβT.
查看答案
考题 设A1，A2分别为m阶，n阶可逆矩阵，分块矩阵.证明：A可逆，且
查看答案
考题 设A,B都是N阶对称矩阵，证明AB是对称矩阵的充分必要条件是.AB=BA
查看答案
考题 设A为m阶实对称矩阵且正定，B为m×n实矩阵，B^T为B的转置矩阵，试证：B^TAB为正定矩阵的充分必要条件是B的秩r(B)=n，
查看答案
考题 设A为n阶正定矩阵,证明：对任意的可逆矩阵P,P^TAP为正定矩阵.
查看答案
考题 设A是n阶矩阵，E+A是可逆矩阵，记，若A按足条件，证明是反对称矩阵。
查看答案
考题 设A为m阶正定矩阵,B为m×n阶实矩阵.证明：B^SAB正定的充分必要条件是r(B)=n,
查看答案
考题 设A为n阶非零矩阵，E为n阶单位矩阵，若A^3=O，则 A.AE-A不可逆，E+A不可逆 B.E-A不可逆，E+A可逆 C.E-A可逆，E+A可逆 D.E-A可逆，E+A不可逆
查看答案
考题 设A为n阶非零矩阵，E为n阶单位矩阵。若A3=0，则( )。A.E－A不可逆，E+A不可逆 B.E—A不可逆。E+A可逆 C.E—A可逆。E+A可逆 D.E—A可逆。E十A不可逆
查看答案
考题 设A为n阶可逆矩阵，则(-A)的伴随矩阵(-A)n等于（ ）。 A. -An B. An C. (-1)nAn D. (-1)n-1An
查看答案
考题 设A为n阶可逆矩阵，则（-A）的伴随矩阵（-A）*等于（）。A、-A*B、A*C、（-1）nA*D、（-1）n-1A*
查看答案
考题 填空题设n维向量α(→)＝（a，0，…，0，a）T，a＜0，E为n阶单位矩阵，矩阵A＝E－α(→)α(→)T，B＝E＋α(→)α(→)T/a，且B为A的逆矩阵，则a＝____。
查看答案
考题 单选题设A为m×n矩阵，B为n×m矩阵，E为m阶单位矩阵，若AB＝E，则（　　）。A r（A）＝m，r（B）＝mB r（A）＝m，r（B）＝nC r（A）＝n，r（B）＝mD r（A）＝n，r（B）＝n
查看答案
考题 单选题设n维行向量α＝（1/2，0，…，0，1/2），矩阵A＝E－αTα，B＝E＋2αTα，其中E为n阶单位矩阵，则AB等于（　　）。A OB －EC ED E＋αTα
查看答案
考题 问答题设A是n阶矩阵，且满足Am＝E，其中m为整数，E为n阶单位矩阵。令将A中的元素aij换成它的代数余子式Aij而成的矩阵为A(～)，证明：（A(～)）m＝E。
查看答案
考题 填空题设A为n阶方阵，E为n阶单位矩阵，且A2＝A，则（A－2E）－1＝____。
查看答案
考题 问答题设A＝E－α(→)α(→)T，其中E是n阶单位矩阵，α(→)是n维非零列向量，α(→)T是α(→)的转置。证明：　　（1）A2＝A的充要条件是α(→)Tα(→)＝1；　　（2）当α(→)Tα(→)＝1时，A是不可逆矩阵。
查看答案
考题 单选题设n维向量α(→)＝（a，0，…，0，a）T，a＜0，E为n阶单位矩阵，矩阵A＝E－α(→)α(→)T，B＝E＋α(→)α(→)T/a，且B为A的逆矩阵，则a＝（　　）。A 4B 2C －1D 1
查看答案
考题 单选题设n维向量α(→)＝（a，0，…，0，a）T，a＜0，E为n阶单位矩阵，矩阵A＝E－α(→)α(→)T，B＝E＋α(→)α(→)T/a，且B为A的逆矩阵，则a＝（　　）。A －1B 1C －2D 2
查看答案
考题 单选题设A为n阶可逆矩阵，则（-A）的伴随矩阵（-A）*等于（）。A -A*B A*C （-1）nA*D （-1）n-1A*
查看答案
热门标签
最新试卷